题目内容
10.若多项式x4+mx3+nx-16含有因式(x-2)和(x-1),则mn的值是( )| A. | 100 | B. | 0 | C. | -100 | D. | 50 |
分析 根据待定系数法进行求解,因为多项式x4+mx3+nx-16的最高次数是4次,所以要求的代数式的最高次数是3次,再根据两个多项式相等,则对应次数的系数相等列方程组求解.
解答 解:设x4+mx3+nx-16=(x-1)(x-2)(x2+ax+b),
则x4+mx3+nx-16=x4+(a-3)x3+(b-3a+2)x2+(2a-3b)x+2b.
比较系数得:$\left\{\begin{array}{l}{a-3=m}\\{b-3a+2=0}\\{2a-3b=n}\\{2b=-16}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-2}\\{b=-8}\\{m=-5}\\{n=20}\end{array}\right.$,
所以mn=-5×20=-100.
故选:C.
点评 此题考查了求多项式中的字母系数的值的问题,能够运用待定系数法以及特殊值法进行求解.

练习册系列答案
相关题目
15.把x2y-2y2x+y3分解因式正确的是( )
| A. | y(x+y)(x-y) | B. | y(x-y)2 | C. | y(x2-2xy+y2) | D. | (x-2y)2 |
2.连续四次抛掷一枚硬币都是正面朝上,则“第五次抛掷正面朝上”是( )
| A. | 必然事件 | B. | 不可能事件 | C. | 随机事件 | D. | 概率为1的事件 |

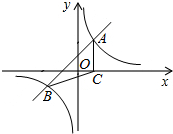 如图,直线y=x+1与双曲线y=$\frac{2}{x}$交于A、B两点,其中A点在第一象限.C为x轴正半轴上一点,且AC⊥x轴于C,P为反比例函数图象上的一点,Q为x轴上的一点.
如图,直线y=x+1与双曲线y=$\frac{2}{x}$交于A、B两点,其中A点在第一象限.C为x轴正半轴上一点,且AC⊥x轴于C,P为反比例函数图象上的一点,Q为x轴上的一点.