题目内容
18. 如图,在?ABCD中,AE平分∠BAD交DC于点E,AD=5cm,AB=8cm.
如图,在?ABCD中,AE平分∠BAD交DC于点E,AD=5cm,AB=8cm.(1)求EC的长.
(2)作∠BCD的平分线交AB于F,求证:四边形AECF为平行四边形.
分析 (1)首先根据角平分线的性质可得∠1=∠3,再根据平行线的性质可得∠3=∠2,利用等量代换可得∠1=∠2,根据等角对等边可得AD=DE,再根据线段的和差关系可得EC长;
(2)首先根据平行四边形的性质可得∠DAB=∠DCB,CD∥AB,再根据角平分线的性质可得∠3=∠ECF,再证明AE∥CF,根据两组对边分别平行的四边形是平行四边形可证明四边形AECF为平行四边形.
解答 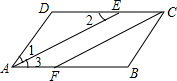 解:(1)∵AE平分∠BAD,
解:(1)∵AE平分∠BAD,
∴∠1=∠3,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠3=∠2,
∴∠1=∠2,
∴AD=DE=5cm,
∵AB=8cm,
∴EC=8-5=3cm;
(2)∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB,CD∥AB,
∵AE平分∠BAD,
∴∠3=$\frac{1}{2}∠DAB$,
∵CF平分∠DCB,
∴∠ECF=$\frac{1}{2}∠DCB$,
∴∠3=∠ECF,
∵∠2=∠3,
∴∠2=∠ECF,
∴AE∥CF,
∴四边形AECF为平行四边形.
点评 此题主要考查了平行四边形的判定和性质,关键是掌握平行四边形两组对边分别平行,两组对边分别平行的四边形是平行四边形.

练习册系列答案
相关题目
8.下列不等式中,属于一元一次不等式的是( )
| A. | 4>1 | B. | 3x-2<4 | C. | $\frac{1}{x}$<2 | D. | 4x-3<2y-7 |
8.下列计算正确的是( )
| A. | (-x-y)2=-x2-2xy-y2 | B. | (4x+1)2=16x2+8x+1 | ||
| C. | (2x-3)2=4x2+12x-9 | D. | (a+2b)2=a2+2ab+4b2 |
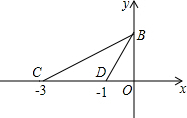 如图,在平面直角坐标系中,C(-3,0),D(-1,0),点B在y轴正半轴上,且tan∠BCO=$\frac{\sqrt{3}}{3}$
如图,在平面直角坐标系中,C(-3,0),D(-1,0),点B在y轴正半轴上,且tan∠BCO=$\frac{\sqrt{3}}{3}$ 如图是一个长方形纸条折成的图形,已知图中∠2=122°,则∠1=116°.
如图是一个长方形纸条折成的图形,已知图中∠2=122°,则∠1=116°.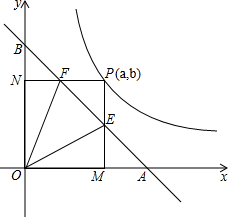 如图,直线与x轴、y轴交于A、B两点,且OA=OB=1,点P是反比例函数$y=\frac{1}{2x}$图象在第一象限的分支上的任意一点,P点坐标为(a,b),由点P分别向x轴,y轴作垂线PM、PN,垂足分别为M、N;PM、PN分别与直线交于点E,点F.
如图,直线与x轴、y轴交于A、B两点,且OA=OB=1,点P是反比例函数$y=\frac{1}{2x}$图象在第一象限的分支上的任意一点,P点坐标为(a,b),由点P分别向x轴,y轴作垂线PM、PN,垂足分别为M、N;PM、PN分别与直线交于点E,点F.