题目内容
 如图,在△ABC中,∠A=80°,∠ABC与∠ACD的平分线交于点E,∠EBC与∠ECD的平分线相交于点F,则∠BFC=
如图,在△ABC中,∠A=80°,∠ABC与∠ACD的平分线交于点E,∠EBC与∠ECD的平分线相交于点F,则∠BFC=考点:三角形内角和定理,三角形的外角性质
专题:
分析:利用角平分线定义可知∠ECD=
∠ACD.再利用外角性质,可得∠ACD=∠A+∠ABC①,∠ECD=∠E+
∠ABC②,那么可利用∠ECA=∠ECD,可得相等关系:∠E=
∠A,从而可求∠E,同理可得:∠F=
∠E,进而求出∠F的度数.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵CE是∠ACD的角平分线,
∴∠ECD=
∠ACD,
又∵∠ACD=∠A+∠ABC,
∴∠ECD=
∠A+
∠ABC,
又∵∠ECD=∠E+
∠ABC,
∴
∠A+
∠ABC=∠E+
∠ABC,
∴∠E=
∠A=40°;
同理:∠F=
∠E=20°,
即:∠BFC=20°.
故答案为:20°.
∴∠ECD=
| 1 |
| 2 |
又∵∠ACD=∠A+∠ABC,
∴∠ECD=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ECD=∠E+
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠E=
| 1 |
| 2 |
同理:∠F=
| 1 |
| 2 |
即:∠BFC=20°.
故答案为:20°.
点评:本题利用了角平分线定义、三角形外角的性质.三角形的外角等于与它不相邻的两个内角之和.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
不透明的布袋中装有红、白、黄和黑4个除颜色外其他都相同的小球,从中任意摸出一个是白色的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
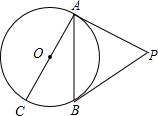 如图所示,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠ACB的度数是( )
如图所示,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠ACB的度数是( )| A、70° | B、40° |
| C、50° | D、20° |
下列说法错误的是(圆周角均指小于平角的角)( )
| A、同弧所对的圆周角相等 |
| B、同弧上的圆周角等于圆心角的一半 |
| C、同弧所对的圆心角相等 |
| D、同弧上的圆心角等于圆周角的一半 |
甲、乙两位同学对代数式
(a>0,b>0),分别作了如下变形:
甲:
=
=
-
乙:
=
=
+
关于这两种变形过程的说法正确的是( )
| a-b | ||||
|
甲:
| a-b | ||||
|
(a-b)(
| ||||||||
(
|
| a |
| b |
乙:
| a-b | ||||
|
(
| ||||||||
|
| a |
| b |
关于这两种变形过程的说法正确的是( )
| A、甲、乙都正确 |
| B、甲、乙都不正确 |
| C、只有甲正确 |
| D、只有乙正确 |
若
-1的倒数是
,则x的值为( )
| 3x+1 |
| 4 |
| 1 |
| 3 |
| A、5 | ||
B、
| ||
C、
| ||
| D、-5 |
 如图,四边形ABCD中,点E、F分别为AB、AD的中点,且EF=3,BC=10,CD=8,求cosC.
如图,四边形ABCD中,点E、F分别为AB、AD的中点,且EF=3,BC=10,CD=8,求cosC.