题目内容
4. 按要求完成下列各小题.
按要求完成下列各小题.(1)已知a,b表示的是等腰三角形两条边的长度,且|4-a|+(b-8)2=0,求该三角形的周长;
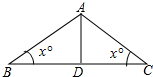
(2)如图,在△ABC中,AD是高,∠BAC=3x°,求∠DAC的度数.
分析 (1)由已知条件、绝对值和偶次方的非负性质得出a=4,b=8,由三角形的三边关系得出a为底边长,b为腰长,即可得出结果;
(2)由三角形内角和定理得出方程,解方程求出x=36,得出∠C的度数,再由直角三角形的两个锐角互余即可得出结果.
解答 解:(1)∵|4-a|+(b-8)2=0,
∴4-a=0,b-8=0,
∴a=4,b=8,
∵4+4=8,
∴a为底边长,b为腰长,
∴等腰三角形的周长=8+8+4=20;
(2)由三角形内角和定理得:x°+x°+3x°=180°,
解得:x=36,
∴∠C=36°,
∵AD是高,
∴AD⊥BC,
∴∠ADC=90°,
∴∠DAC=90°-∠C=54°.
点评 本题考查了等腰三角形的性质、三角形的三边关系、绝对值和偶次方的非负性质以及三角形内角和定理;熟练掌握等腰三角形的性质和三角形的三边关系,由三角形内角和定理得出方程是解决(2)的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.在Rt△ABC中,AD为斜边上的高,S△ABC=4S△ABD,则cosB=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{\sqrt{3}}{2}$ |
12.将抛物线y=x2+1先向左平移2个单位,再向下平移4个单位,那么所得到的抛物线的函数关系式是( )
| A. | y=(x+2)2+3 | B. | y=(x+2)2-3 | C. | y=(x-2)2+3 | D. | y=(x-2)2-3 |
19.某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2014年县政府已投资4亿元人民币.若每年投资的增长率相同,预计2016年投资5.76亿元人民币,那么每年投资的增长率为( )
| A. | 40% | B. | 20% | C. | -220% | D. | 30% |
14.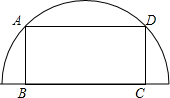 如图,一个长为2、宽为1的矩形ABCD内接于半圆O,矩形的长BC在半圆半径上,则半圆O的面积为( )
如图,一个长为2、宽为1的矩形ABCD内接于半圆O,矩形的长BC在半圆半径上,则半圆O的面积为( )
 如图,一个长为2、宽为1的矩形ABCD内接于半圆O,矩形的长BC在半圆半径上,则半圆O的面积为( )
如图,一个长为2、宽为1的矩形ABCD内接于半圆O,矩形的长BC在半圆半径上,则半圆O的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
 如图,梯形ABCD绕O点旋转后,顶点C的对应点为C′点,试确定顶点A,B,D对应点的位置,以及旋转后的梯形A′B′C′D′.
如图,梯形ABCD绕O点旋转后,顶点C的对应点为C′点,试确定顶点A,B,D对应点的位置,以及旋转后的梯形A′B′C′D′.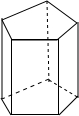 如图所示的五棱柱的底面边长都是5cm,侧棱长12cm,它有多少个面?它的所有侧面的面积之和是多少?
如图所示的五棱柱的底面边长都是5cm,侧棱长12cm,它有多少个面?它的所有侧面的面积之和是多少? 如图,∠1=∠C,AC平分∠DAB,求证:DC∥AB.
如图,∠1=∠C,AC平分∠DAB,求证:DC∥AB.