题目内容
14.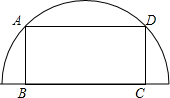 如图,一个长为2、宽为1的矩形ABCD内接于半圆O,矩形的长BC在半圆半径上,则半圆O的面积为( )
如图,一个长为2、宽为1的矩形ABCD内接于半圆O,矩形的长BC在半圆半径上,则半圆O的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | 2π |
分析 由于矩形的长BC在半圆半径上,故C的中点O即为半圆的圆心,过点O作OE⊥AD,连接OD,根据垂径定理求出DE的长,再由勾股定理得出OD的长,根据圆的面积公式即可得出结论.
解答 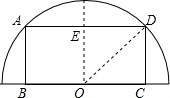 解:∵矩形的长BC在半圆半径上,
解:∵矩形的长BC在半圆半径上,
∴C的中点O即为半圆的圆心.
过点O作OE⊥AD,连接OD,
∵AD=2,CD=1,
∴DE=$\frac{1}{2}$AD=1,
∴OD=$\sqrt{{DE}^{2}+{OE}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴S半圆=$\frac{1}{2}$π×($\sqrt{2}$)2=π.
故选C.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.当式子|x-1|+|x-2|+|x-3|+…+|x-1999|取得最小值时,实数x的值是( )
| A. | 1 | B. | 999 | C. | 1000 | D. | 1999 |
 按要求完成下列各小题.
按要求完成下列各小题.