题目内容
2.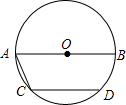 如图,AB是⊙O直径,CD是弦,AB∥CD,且AB=30cm,CD=24cm,求弦AC的长.
如图,AB是⊙O直径,CD是弦,AB∥CD,且AB=30cm,CD=24cm,求弦AC的长.
分析 作OE⊥CD于E,CF⊥AB于F,连接OC,根据垂径定理得出CE=DE=$\frac{1}{2}$CD=12cm,根据勾股定理求得OE,即可求得CF,然后根据勾股定理求得AC即可.
解答 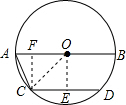 解:作OE⊥CD于E,CF⊥AB于F,连接OC,
解:作OE⊥CD于E,CF⊥AB于F,连接OC,
∴CF∥OE,CE=DE=$\frac{1}{2}$CD=12cm,
∵OC=OA=OB=$\frac{1}{2}$AB=15cm,
∴OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=9cm,
∵CF∥OE,AB∥CD,
∴四边形CEOF是平行四边形,
∴CF=OE=9cm,
∵AF=$\frac{1}{2}$(AB-CD)=3cm,
在RT△ACF中,AC=$\sqrt{C{F}^{2}+A{F}^{2}}$=3$\sqrt{10}$cm.
点评 本题考查了垂径定理和勾股定理的应用以及平行四边形的判定和性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
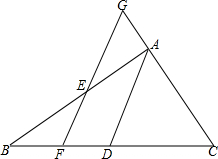 如图,在△ABC中,D是BC的中点,E是线段上的一个动点,(与A、B不重合)过E作AD的平行线,分别与CA的延长线交于G,和BC边交于点F
如图,在△ABC中,D是BC的中点,E是线段上的一个动点,(与A、B不重合)过E作AD的平行线,分别与CA的延长线交于G,和BC边交于点F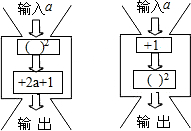 分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?
分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?