题目内容
13.(1)解方程:3(x-1)3-1=80;(2)已知一个正数的平方根是a+3与2a-15,求a的值;
(3)已知x,y为实数,且y=$\sqrt{x-9}-\sqrt{9-x}$+4,求$\sqrt{x}$+$\sqrt{y}$的值.
分析 (1)方程整理后,利用立方根定义开立方即可求出解;
(2)根据正数的平方根有2个,且互为相反数求出a的值即可;
(3)利用负数没有平方根求出x的值,进而确定出y的值,即可求出原式的值.
解答 解:(1)方程整理得:(x-1)3=27,
开立方得:x-1=3,
解得:x=4;
(2)根据平方根的性质得,a+3+2a-15=0,
解得:a=4;
(3)满足二次根式$\sqrt{x-9}$与$\sqrt{9-x}$有意义,则$\left\{\begin{array}{l}{x-9≥0}\\{9-x≥0}\end{array}\right.$,
解得:x=9,
∴y=0-0+4=4,
∴原式=3+2=5.
点评 此题考查了立方根,平方根,以及二次根式有意义的条件,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
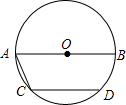 如图,AB是⊙O直径,CD是弦,AB∥CD,且AB=30cm,CD=24cm,求弦AC的长.
如图,AB是⊙O直径,CD是弦,AB∥CD,且AB=30cm,CD=24cm,求弦AC的长. 如图,a,b,c是数轴上三个点A、B、C所对应的实数,|a|<|c|,试化简:($\sqrt{c}$)2+|a-b|+$\root{3}{(a+b)^{3}}$-|a+c|
如图,a,b,c是数轴上三个点A、B、C所对应的实数,|a|<|c|,试化简:($\sqrt{c}$)2+|a-b|+$\root{3}{(a+b)^{3}}$-|a+c|