题目内容
13.先化简(1-$\frac{1}{x-1}$)÷$\frac{{x}^{2}-4x+4}{{x}^{2}-1}$,然后从-1,0,1这三个数中选取一个合适的数作为x的值代入求值.分析 首先对括号内内的式子通分相减,把除法转化为乘法,计算乘法即可化简,然后根据分式有意义的条件确定x的值,然后代入求值即可.
解答 解:原式=$\frac{x-2}{x-1}$•$\frac{(x+1)(x-1)}{(x-2)^{2}}$
=$\frac{x+1}{x-2}$.
若分式有意义,则x只能取0.
则当x=0时,原式=-$\frac{1}{2}$.
点评 本题考查了分式的化简求值,正确对分式的分子和分母正确进行分解因式是关键.

练习册系列答案
相关题目
3.丽水市某一周每天的最高气温统计如下(单位:℃):24,26,28,30,28,28,26,则这组数据的众数与中位数分别是( )
| A. | 28,30 | B. | 28,28 | C. | 28,26 | D. | 26,28 |
19. 如图,在四边形ABCD中,∠C=110°,与∠BAD,∠ABC相邻的外角都是120°,则∠ADC的外角α的度数是( )
如图,在四边形ABCD中,∠C=110°,与∠BAD,∠ABC相邻的外角都是120°,则∠ADC的外角α的度数是( )
 如图,在四边形ABCD中,∠C=110°,与∠BAD,∠ABC相邻的外角都是120°,则∠ADC的外角α的度数是( )
如图,在四边形ABCD中,∠C=110°,与∠BAD,∠ABC相邻的外角都是120°,则∠ADC的外角α的度数是( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
 ,则m的值是( )
,则m的值是( )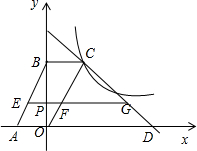 如图,在平面直角坐标系中,四边形ABCO是平行四边形,点O为坐标原点,点A的坐标为(-2,0),点B在y轴的正半轴上,点C在双曲线y=-$\frac{8}{x}$上,直线y=-x+m经过点C,交x轴于点D.
如图,在平面直角坐标系中,四边形ABCO是平行四边形,点O为坐标原点,点A的坐标为(-2,0),点B在y轴的正半轴上,点C在双曲线y=-$\frac{8}{x}$上,直线y=-x+m经过点C,交x轴于点D. 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC向左平移2个单位后得到△A1B1C1.
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC向左平移2个单位后得到△A1B1C1.