题目内容
5.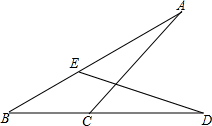 如图,已知AC=DE,AB=BD,求证:BC=BE.
如图,已知AC=DE,AB=BD,求证:BC=BE.
分析 作AM⊥BD于M,DN⊥AB于N,先证明△ABM≌△DBN得AM=DN,BM=BN,再证明△ACM≌△DEN得CM=EN即可证明.
解答 证明:作AM⊥BD于M,DN⊥AB于N,则∠AMB=∠DNB=90°
在△ABM和△DBN中,
$\left\{\begin{array}{l}{∠B=∠B}\\{∠AMB=∠DNB}\\{AB=BD}\end{array}\right.$,
∴△ABM≌△DBN,
∴AM=DN,BM=BN
在RT△ACM和RT△DEN中,
$\left\{\begin{array}{l}{AC=DE}\\{AM=DN}\end{array}\right.$,
∴△ACM≌△DEN,
∴CM=EN,
∴BM-CM=BN-EN,即BC=EB
点评 本题考查全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解决问题的关键,学会添加辅助线的方法,本题用了两次全等,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知实数a、b、c满足a+b+c=0,a>b>c,若直线y1=ax+b+c经过抛物线y2=ax2+bx+c的顶点,则下列结论错误的是( )
| A. | 直线y1经过一、三、四象限 | |
| B. | 抛物线y2必经过点(1,0) | |
| C. | 当x>1或x<0时,y2>y1 | |
| D. | 当x>-1时,y1、y2均随x的增大而增大 |
16. 规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
 规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )| A. | (2$\sqrt{3}$,30°) | B. | (60°,2$\sqrt{3}$) | C. | (30°,4) | D. | (30°,2$\sqrt{3}$) |
15.制动距离是汽车处于某一时速的情况下,从开始刹车制动到汽车完全静止时,车辆所开过的路程,对某辆汽车进行测试时,汽车的行驶速度与汽车的制动距离的数据如表所示
(1)该汽车的制动距离s是变量还是常量?
(2)若s是v的一次函数,求s关于v的函数解析式.
| 汽车行驶速度v(千米/小时) | 30 | 40 | 50 | 60 | 70 |
| 制动距离s(米) | 5 | 12 | 19 | 26 | 33 |
(2)若s是v的一次函数,求s关于v的函数解析式.
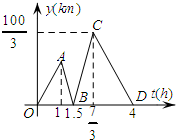 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题:
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题: