题目内容
6.不等式组$\left\{\begin{array}{l}{5x+8>3(x+1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$的最大整数解为4.分析 分别求出每一个不等式的解集,根据口诀:大小小大中间找确定不等式组的解集即可得出答案.
解答 解:解不等式①可得:x>-$\frac{5}{2}$,
解不等式②可得:x≤4,
则不等式组的解集为-$\frac{5}{2}$<x≤4,
∴不等式组的最大整数解为4,
故答案为:4.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
17.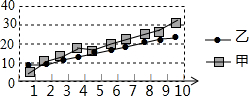 某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
 某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )
某赛季甲、乙两面运动员各参加10场比赛,各场得分情况如图,下列四个结论中,正确的是( )| A. | 甲得分的平均数小于乙得分的平均数 | |
| B. | 甲得分的中位数小于乙得分的中位数 | |
| C. | 甲得分的方差大于乙得分的方差 | |
| D. | 甲得分的最小值大于乙得分的最小值 |
15.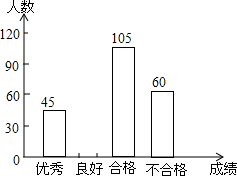 为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
(1)该校初三学生共有多少人?
(2)求表中a,b,c的值,并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
 为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:
为了解今年初三学生的数学学习情况,某校对上学期的数学成绩作了统计分析,绘制得到如下图表.请结合图表所给出的信息解答下列问题:| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
(2)求表中a,b,c的值,并补全条形统计图.
(3)初三(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.
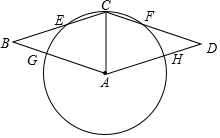 如图,菱形ABCD,以A为圆心,AC长为半径的圆分别交边BC,DC,AB,AD于点E,F,G,H.
如图,菱形ABCD,以A为圆心,AC长为半径的圆分别交边BC,DC,AB,AD于点E,F,G,H.