题目内容
16.两块全等的三角板ABC和EDC如图(1)放置,AC=CB,CE=CD,∠ACB=∠ECD=90°,且AB与CE交于F,ED与AB、BC分别交于M、H,△ABC不动,将△EDC绕点C旋转到如图(2),当∠BCE=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.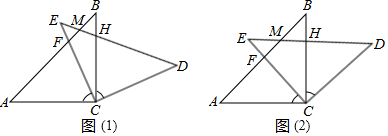
分析 根据△EDC绕点C旋转到∠BCE=45°,推出四边形ACDM是平行四边形,由AC=CD判断出四边形ACDM是菱形.
解答  解:四边形ACDM是菱形.
解:四边形ACDM是菱形.
证明:∵∠ACB=∠DCE=90°,∠BCE=45°,
∴∠1=∠2=45°.
∵∠E=45°,
∴∠1=∠E,
∴AC∥DE,
∴∠AMH=180°-∠A=135°=∠ACD,
又∵∠A=∠D=45°,
∴四边形ACDM是平行四边形(两组对角分别相等的四边形是平行四边形),
∵AC=CD,
∴四边形ACDM是菱形.
点评 本题考查的是旋转的性质以及菱形的判定,熟知图形旋转的性质是解答此题的关键.解题时注意:一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
4.计算(x+2)2,正确的是( )
| A. | x2+4 | B. | x2+2 | C. | x2+4x+4 | D. | 2x+4 |
8.济南园博园对2016年国庆黄金周七天假期的游客人数进行了统计,如表:
其中平均数和中位数分别是( )
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 旅游人数(万) | 1.5 | 2.2 | 2.2 | 3.8 | 1.5 | 2.2 | 0.6 |
| A. | 2和2.2 | B. | 2和2 | C. | 1.5和2.2 | D. | 2.2和3.8 |
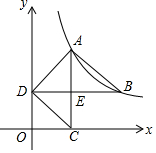 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A(2,4),B(m,n)(m>2)两点,作AC∥y轴交x轴于C,BD∥x轴交y轴于D,AC与BD相交于E,连接AB、AD、CD.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过A(2,4),B(m,n)(m>2)两点,作AC∥y轴交x轴于C,BD∥x轴交y轴于D,AC与BD相交于E,连接AB、AD、CD.