题目内容
14.已知直线AB的解析式为:y=2x-4,(1)当y>-4时,求x得取值范围;
(2)当-2≤x≤4时,求y的取值范围;
(3)已知存在另一直线CD,其解析式为:y=3x+m,若直线AB,CD交于点E,且E在第四象限,求此时m的取值范围.
分析 (1)根据y>-4可得出2x-4>-4,解之即可得出结论;
(2)分别求出当x=-2、4时的y值,由此即可得出当-2≤x≤4时,y的取值范围;
(3)根据一次函数图象上点的坐标特征求出直线AB与两坐标轴的交点坐标,分别将该两点坐标代入直线CD的解析式中求出m值,再结合图形即可得出结论.
解答 解:(1)当y>-4时,有2x-4>-4,
解得:x>0.
(2)当x=-2时,y=2x-4=-8;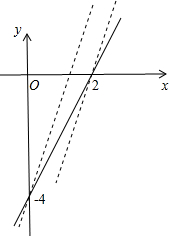
当x=4时,y=2x-4=4.
∴当-2≤x≤4时,-8≤y≤4.
(3)当x=0时,y=2x-4=-4,
∴直线AB与y轴的交点坐标为(0,-4);
当y=2x-4=0时,x=2,
∴直线AB与x轴的交点坐标为(2,0).
当点(0,-4)在直线CD上时,
m=-4;
当点(2,0)在直线CD上时,
6+m=0,
解得:m=-6.
∴若直线AB,CD交于点E,且E在第四象限,则m的取值范围为-6<m<-4.
点评 本题考查了一次函数与一元一次不等式、一次函数图象上点的坐标特征以及一次函数的性质,解题的关键是:(1)根据y>-4找出2x-4>-4;(2)分别求出当x=-2、4时的y值;(3)利用一次函数图象上点的坐标特征求出直线AB与两坐标轴的交点坐标.

练习册系列答案
相关题目
4.计算(x+2)2,正确的是( )
| A. | x2+4 | B. | x2+2 | C. | x2+4x+4 | D. | 2x+4 |
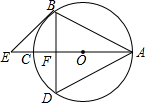 如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点
如图,AC为⊙O的直径,AB=BD,BD交AC于F,BE∥AD交AC的延长线于E点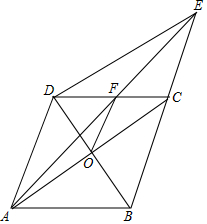 已知:如图,?ABCD中,对角线AC,BD相交于点O,延长BC至E,使CE=BC,连接AE交CD于点F.
已知:如图,?ABCD中,对角线AC,BD相交于点O,延长BC至E,使CE=BC,连接AE交CD于点F.