题目内容
8.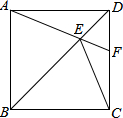 如图,正方形ABCD中,∠DAF=20°,AF交对角线BD于E,交CD于F,则∠BEC=( )
如图,正方形ABCD中,∠DAF=20°,AF交对角线BD于E,交CD于F,则∠BEC=( )| A. | 80° | B. | 70° | C. | 65° | D. | 60° |
分析 根据四边形ABCD是正方形,证出△AED≌△CED,得出∠ECD=∠DAF=20°,再根据角平分线的性质得出∠CDE=45°,最后根据三角形内角和定理求出∠CED的度数,进而求出答案.
解答 解:∵四边形ABCD是正方形,
∴AD=CD,∠ADE=∠CDE,
在△AED和△CED中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDE}\\{DE=DE}\end{array}\right.$,
∴△AED≌△CED,
∴∠ECD=∠DAF=20°,
∵∠CDE=45°,
∴∠CED=180°-20°-45°=115°,
∴∠BEC=180°-115°=65°.
故选C.
点评 本题主要考查了正方形的性质,全等三角形的判定与性质,掌握正方形的每条对角线平分一组对角是解题的关键,此题是一道常考题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.如果两条直线被第三条直线所截,那么一组内错角的平分线( )
| A. | 互相垂直 | B. | 互相平行 | C. | 互相重合 | D. | 不能确定 |
13.计算:22014-(-2)2015的结果是( )
| A. | 22015 | B. | 22014 | C. | -22014 | D. | 3×22014 |