题目内容
18.比较大小:$\sqrt{8}$<$\sqrt{10}$.(填“>”“<”或“=”)分析 首先分别求出$\sqrt{8}$、$\sqrt{10}$的平方各是多少;然后根据实数大小比较的方法,判断出$\sqrt{8}$、$\sqrt{10}$的平方的大小关系,即可判断出$\sqrt{8}$、$\sqrt{10}$的大小关系.
解答 解:${(\sqrt{8})}^{2}$=8
${(\sqrt{10})}^{2}$=10
∵8<10,
∴$\sqrt{8}$<$\sqrt{10}$.
故答案为:<.
点评 (1)此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
(2)解答此题的关键是比较出两个数的平方的大小关系.

练习册系列答案
相关题目
8.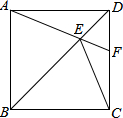 如图,正方形ABCD中,∠DAF=20°,AF交对角线BD于E,交CD于F,则∠BEC=( )
如图,正方形ABCD中,∠DAF=20°,AF交对角线BD于E,交CD于F,则∠BEC=( )
 如图,正方形ABCD中,∠DAF=20°,AF交对角线BD于E,交CD于F,则∠BEC=( )
如图,正方形ABCD中,∠DAF=20°,AF交对角线BD于E,交CD于F,则∠BEC=( )| A. | 80° | B. | 70° | C. | 65° | D. | 60° |
6.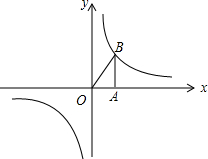 反比例函数y=$\frac{1-m}{x}$的图象如图所示,以下结论正确的是( )
反比例函数y=$\frac{1-m}{x}$的图象如图所示,以下结论正确的是( )
①常数m<1;
②y随x的增大而减小;
③若A为x轴上一点,B为反比例函数上一点,则S△ABC=$\frac{1-m}{2}$;
④若P(x,y)在图象上,则P′(-x,-y)也在图象上.
 反比例函数y=$\frac{1-m}{x}$的图象如图所示,以下结论正确的是( )
反比例函数y=$\frac{1-m}{x}$的图象如图所示,以下结论正确的是( )①常数m<1;
②y随x的增大而减小;
③若A为x轴上一点,B为反比例函数上一点,则S△ABC=$\frac{1-m}{2}$;
④若P(x,y)在图象上,则P′(-x,-y)也在图象上.
| A. | ①②③ | B. | ①③④ | C. | ①②③④ | D. | ①④ |
7.在?ABCD中,对角线AC和BD相交于点O,若AC=8,BD=6,则AB的长不可能是( )
| A. | 1 | B. | 2 | C. | 5 | D. | 6 |
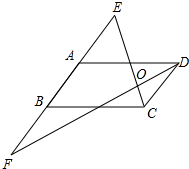 如图所示,在?ABCD中,2AB=AD,AB=AE=BF,求证:EC⊥DF.
如图所示,在?ABCD中,2AB=AD,AB=AE=BF,求证:EC⊥DF.