题目内容
5.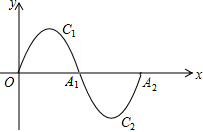 如图,在平面直角坐标系中有一段抛物线C1:y=-x(x-3)(0≤x≤3),与x轴交于点O,A1,交抛物线C1绕点A1旋转180°得C2,交x轴于点A2.
如图,在平面直角坐标系中有一段抛物线C1:y=-x(x-3)(0≤x≤3),与x轴交于点O,A1,交抛物线C1绕点A1旋转180°得C2,交x轴于点A2.(1)填空:抛物线C1的顶点坐标为($\frac{3}{2}$,$\frac{9}{4}$),抛物线C2的顶点坐标为($\frac{9}{2}$,-$\frac{9}{4}$).
(2)求出抛物线C2的解析式.
分析 (1)根据顶点坐标公式:(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),可得答案,再根据顶点关于A1对称,可得答案;
(2)根据旋转的性质:不改变图形的形状,可得答案.
解答 解:(1)y=-x(x-3)的顶点坐标为($\frac{3}{2}$,$\frac{9}{4}$),A1(3,0),
C2横坐标2×3-$\frac{3}{2}$=$\frac{9}{2}$,纵坐标2×0-$\frac{9}{4}$=-$\frac{9}{4}$,C2($\frac{9}{2}$,-$\frac{9}{4}$);
故答案为:($\frac{3}{2}$,$\frac{9}{4}$),($\frac{9}{2}$,-$\frac{9}{4}$);
(2)C2的解析式为y=(x-$\frac{9}{2}$)2-$\frac{9}{4}$.
点评 本题考查了二次函数图象与几何变换,利用了顶点坐标公式:(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),又利用了旋转的性质:不改变图形的形状.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
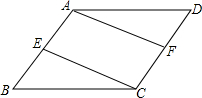 如图,在菱形ABCD中,E,F分别是AB和CD的中点,连接AF,CE.
如图,在菱形ABCD中,E,F分别是AB和CD的中点,连接AF,CE. 已知:A、B、C三点及线段a,如图,求作:点P,使PA=PB,PC=a.
已知:A、B、C三点及线段a,如图,求作:点P,使PA=PB,PC=a.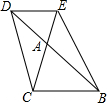 如图,△ABC与△ADE是位似三角形.
如图,△ABC与△ADE是位似三角形.