题目内容
20.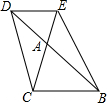 如图,△ABC与△ADE是位似三角形.
如图,△ABC与△ADE是位似三角形.(1)判断BC与DE的位置关系;
(2)若AE=2,AC=4,AD=3,求△ADE与△ABC的相似比及AB的长度.
分析 (1)直接利用位似图形的性质得出对应边关系即可;
(2)利用位似图形的性质得出对应边的比以及AB的长.
解答 解:(1)∵△ABC与△ADE是位似三角形,
∴BC∥DE;
(2)∵△ABC与△ADE是位似三角形,
∴△ABC∽△ADE,
∴$\frac{AE}{AC}$=$\frac{DA}{AB}$,
∴$\frac{2}{4}$=$\frac{3}{AB}$=$\frac{1}{2}$,
解得:AB=6,
∴△ADE与△ABC的相似比为:1:2,
AB的长度为6.
点评 此题主要考查了位似变换以及相似三角形的性质,正确应用位似图形的性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.用配方法解一元二次方程x2-6x+4=0,下列变形正确的是( )
| A. | (x-3)2=13 | B. | (x-3)2=5 | C. | (x-6)2=13 | D. | (x-6)2=5 |
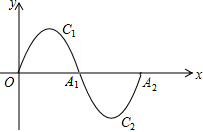 如图,在平面直角坐标系中有一段抛物线C1:y=-x(x-3)(0≤x≤3),与x轴交于点O,A1,交抛物线C1绕点A1旋转180°得C2,交x轴于点A2.
如图,在平面直角坐标系中有一段抛物线C1:y=-x(x-3)(0≤x≤3),与x轴交于点O,A1,交抛物线C1绕点A1旋转180°得C2,交x轴于点A2.