题目内容
14.在同一平面直角坐标系中,直线y=2x+1与双曲线y=$\frac{k}{x}$(k≠0)只有一个交点.(1)求k的值;
(2)求这个交点的坐标.
分析 (1)联立两函数方程,解一元二次方程,求根的判别式,即可得出结果.
(2)把k的值代入2x2+x-k=0,解方程求得x的值,然后打印y=2x+1,即可求得交点坐标.
解答 解:(1)∵直线y=2x+1与双曲线y=$\frac{k}{x}$(k≠0)只有一个交点,
∴2x+1=$\frac{k}{x}$,
2x2+x-k=0,
∴1+8k=0,
解得k=-$\frac{1}{8}$.
(2)∵k=-$\frac{1}{8}$,
∴2x2+x+$\frac{1}{8}$=0,
∴x1=x2=-$\frac{1}{4}$,
∴y=2x+1=2×(-$\frac{1}{4}$)+1=$\frac{1}{2}$,
∴交点的坐标(-$\frac{1}{4}$,$\frac{1}{2}$).
点评 本题综合考查反比例函数和一次函数的交点问题,掌握求函数图象交点的方法是解题的关键,即联立两函数解析式求其方程组的解.

练习册系列答案
相关题目
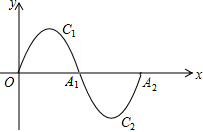 如图,在平面直角坐标系中有一段抛物线C1:y=-x(x-3)(0≤x≤3),与x轴交于点O,A1,交抛物线C1绕点A1旋转180°得C2,交x轴于点A2.
如图,在平面直角坐标系中有一段抛物线C1:y=-x(x-3)(0≤x≤3),与x轴交于点O,A1,交抛物线C1绕点A1旋转180°得C2,交x轴于点A2. 在△ABC中,∠C=90°,AC=7,BC=24,求sinA,sinB的值.
在△ABC中,∠C=90°,AC=7,BC=24,求sinA,sinB的值.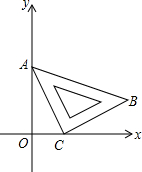 在平面直角坐标系中,将一块为等腰Rt△ABC的三角板按如图所示放置,若AO=2,OC=1,∠ACB=90°.
在平面直角坐标系中,将一块为等腰Rt△ABC的三角板按如图所示放置,若AO=2,OC=1,∠ACB=90°.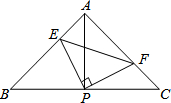 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论: