题目内容

5．若103•102n+1=102014，求n的值．

分析 先将左边根据同底数幂的乘法变形为103+2n+1，将等式的左边和右边化为同底数幂的形式，则指数相等，形式可得n的值．

解答 解：103•102n+1=102014，
103+2n+1=102014，
∴3+2n+1=2014，
n=1005．

点评 本题考查了同底数幂的乘法，利用同底数幂的乘法化成底数相同的幂是解题关键．

练习册系列答案
相关题目
19．已知2m=a，32n=b，求23m+10n的值．
20．点A及点B的坐标分别为（-2，6）及（3，8）．A向下平移13单位至A′，B绕原点顺时针方向旋转90°至B′．
（a）写出A′及B′的坐标
（b）证明AB平行于A′B′．
17．计算（-3$\frac{1}{3}$）2-$\frac{4}{13}$×（-6.5）+（-2）6÷（-6）=2$\frac{4}{9}$．
4．我国是世界上严重缺水的国家之一．为了增强居民的节水意识，某市自来水公司对居民用水采用以户为单位分段计费的办法收费．即一个月用水10吨以内（包括10吨）的用户，每吨收水费a元；一个月用水超过10吨的用户，10吨水仍按每吨a元收费，超过10吨的部分，按每吨b元（b＞a）收费．设一户居民月用水x吨，应收水费y元，y与x之间的函数关系如图：
（1）求a的值，并求一个月用水8吨时的水费；
（2）求b的值，并写出当x≥10时，y与x之间的函数关系式．
10．某同学计算：（-$\frac{1}{30}$）÷（$\frac{2}{3}$-$\frac{1}{10}$+$\frac{1}{6}$-$\frac{2}{5}$）的过程如下：
解：原式=（-$\frac{1}{30}$）÷$\frac{2}{3}$+（-$\frac{1}{30}$）÷（$\frac{1}{10}$）+（$\frac{1}{30}$）÷$\frac{1}{6}$+（-$\frac{1}{30}$）÷（-$\frac{2}{5}$）
=（-$\frac{1}{30}$）×$\frac{3}{2}$+（-$\frac{1}{30}$）×（-10）+（-$\frac{1}{30}$）×6+（-$\frac{1}{30}$）×（-$\frac{5}{2}$）
审视上述解法是否正确？如果不正确，指出错误在哪里？并给出正确的过程．
17．a12÷a6=a6；
用小数表示3.14×10-4=0.000314．
14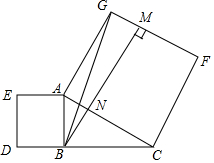．如图，在Rt△ABC中，∠ABC=90°，分别以AB、AC为边向外作正方形ABDE和正方形ACFG，过点B作BM⊥GF，垂足为M，BM交AC于点N，连接BG，CE，下列结论中，不正确的是（　　）
A．BG=CEB．BG⊥CE
C．S正方形ABDE＞S四边形ANMGD．BC2=CF•FM
15．已知关于x的一元二次方程ax2+bx-6=0与ax2+2bx-15=0有一个公共根是3．求a，b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网