题目内容
16．图①、图②都是6×6的正方形网格，每个小正方形的边长均为1，每个小正方形顶点叫做格点，点A、B、C都在格点上，按要求完成下列画图．（1）请在图①中找到格点D，使四边形ABCD只是中心对称图形，并画出这个四边形；
（2）请在图②中找到格点E，使以A、B、C、E为顶点的四边形既是轴对称图形又是中心对称图形，并画出这个四边形．
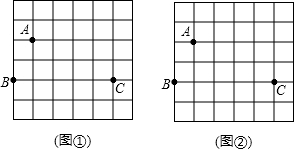
分析 （1）画一个平行四边形，则是中心对称图形，而不是轴对称图形；
（2）画一个矩形，则既是中心对称图形，又是轴对称图形．
解答 解：（1）如图①所示：
（2）如图②所示：
点评 本题主要考查作图-旋转变换，作图-轴对称变换，轴对称图形和中心对称图形的判定，掌握常见图形的对称性是解题的关键．
练习册系列答案
相关题目
6．
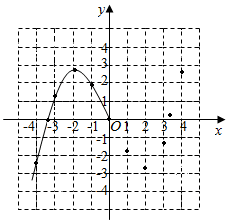某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时，已列表、描点并画出了图象的一部分．
（1）请补全函数图象；
（2）方程$\frac{1}{6}$x3-2x=-2实数根的个数为3；
（3）观察图象，写出该函数的两条性质．
某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时，已列表、描点并画出了图象的一部分．| x | … | -4 | -3.5 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
| y | … | -$\frac{8}{3}$ | -$\frac{7}{48}$ | $\frac{3}{2}$ | $\frac{8}{3}$ | $\frac{11}{6}$ | 0 | -$\frac{11}{6}$ | -$\frac{8}{3}$ | -$\frac{3}{2}$ | $\frac{7}{48}$ | $\frac{8}{3}$ | … |
（2）方程$\frac{1}{6}$x3-2x=-2实数根的个数为3；
（3）观察图象，写出该函数的两条性质．
根据图中各点的位置，在数轴上A，B，C，D四个点中，其中表示的数与4-$\sqrt{28}$的结果最接近的点是B．
11．某种品牌的洗面奶，外包装标明净含量为500±10g，表明了这种洗面奶的净含量x的范围是（ ）
| A． | 490＜x＜510 | B． | 490≤x≤510 | C． | 490＜x≤510 | D． | 490≤x＜510 |
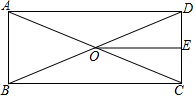如图，在矩形ABCD中，对角线AC与BD交于点O，E为CD的中点，连接OE，若AB=5，BC=12，则四边形BCEO的周长为27．
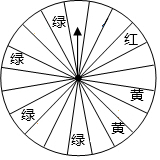某商场为了吸引顾客，设立了一个可以自由转动的转盘（转盘被等分成20个扇形，如图）并规定：顾客在本商场每消费200元，就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准红、黄或绿色区域，顾客就可以分别获得100元、50元、20元的购物券．某顾客消费210元，他转动转盘获得购物券的概率是多少？他得到100元、50元、20元购物券的概率分别是多少？