题目内容
1．
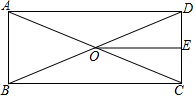如图，在矩形ABCD中，对角线AC与BD交于点O，E为CD的中点，连接OE，若AB=5，BC=12，则四边形BCEO的周长为27．
分析 由矩形的性质和勾股定理求出AC，再证明OE是△BCD的中位线，得出OE=$\frac{1}{2}$BC=6，即可得出四边形BCEO的周长．
解答 解：∵四边形ABCD是矩形，
∴∠ABC=90°，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=13，
∴BD=13，
∴OB=6.5，
∵E是CD的中点，
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}$AB=2.5，OE=$\frac{1}{2}$BC=6，
∴四边形BCEO的周长=BC+CE+EO+BO=12+2.5+6+6.5=27．
故答案为：27．
点评 本题考查了矩形的性质、三角形中位线定理、勾股定理；熟练掌握矩形的性质，并能进行推理计算是解决问题的关键．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE．
9．为了保护环境，某企业决定购买10台污水处理设备，现有A，B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如表．
预算要求，该企业购买污水处理设备的资金不高于105万元．
（1）请问该企业有几种购买方案；
（2）若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；
（3）实际上，该企事业污水的处理方式有两种：A．交污水厂处理厂处理；B．企业购买设备自行处理．如果污水厂处理厂处理污水每吨收费10元，在第（2）问的条件下，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？
| A型 | B型 | |
| 价格（万元/台） | 12 | 10 |
| 处理污水量（吨/月） | 240 | 200 |
| 年消耗费（万元/台） | 1 | 1 |
（1）请问该企业有几种购买方案；
（2）若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；
（3）实际上，该企事业污水的处理方式有两种：A．交污水厂处理厂处理；B．企业购买设备自行处理．如果污水厂处理厂处理污水每吨收费10元，在第（2）问的条件下，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？
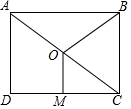如图，点O是矩形ABCD的对角线AC的中点，M是CD边的中点．若AB=8，OM=3，则线段OB的长为5．