题目内容
12.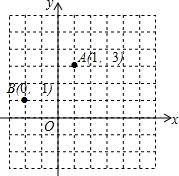 如图,在边长为1的网格中有一个平面直角坐标系.
如图,在边长为1的网格中有一个平面直角坐标系.(1)若点B是A为顶点的抛物线上一点,试在图中画中抛物线的对称轴,并写出点B在抛物线上的对称点的坐标;
(2)试在图中画出这条抛物线;
(3)若x1<x2<x3<1,试确定它们对应的函数值y1,y2,y3的大小,并用“<”号连接;
(4)写出抛物线的表达式.
分析 (1)由A的坐标可知对称轴为直线x=1,画出直线x=1,根据轴对称的性质即可求得B的对称点的坐标;
(2)在坐标系作出抛物线即可;
(3)根据抛物线的性质即可求得;
(4)根据待定系数法即可求得.
解答 解:(1)如图1.画出对称轴,点B在抛物线上的对称点的坐标为(4,1);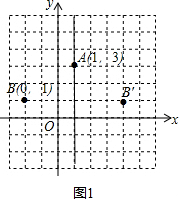
(2)画出抛物线如图2所示: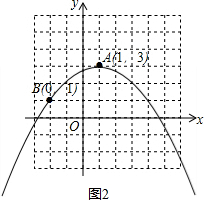
(3)在对称轴x=1的左侧y随x的证得而增大,
∵x1<x2<x3<1,
∴y1<y2<y3;
(4)设顶点式为y=a(x-1)2+3,
代入点(-2,1),得1=a(-2-1)2+3,
解得a=-$\frac{2}{9}$,
∴抛物线的表达式为y=-$\frac{2}{9}$(x-1)2+3.
点评 本题考查了二次函数的图象,二次函数图象上点的坐标特征,待定系数法求二次函数的解析式,熟练掌握待定系数法以及二次函数的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列运算结果为正数的是( )
| A. | 1-24×5 | B. | -24×5 | C. | (-2)4×5 | D. | 1-24 |
17.解方程(x+1)(x+3)=5较为合适的方法( )
| A. | 直接开平方法 | B. | 配方法 | C. | 公式法或配方法 | D. | 分解因式法 |
4.一艘轮船从港口A出发向东北方向航行7km,另一艘轮船也从港口A出发向东南方向航行了12km,此时两艘轮船相距( )
| A. | 5km | B. | $\sqrt{193}$km | C. | 19km | D. | 193km |
1.抛物线y=$\frac{1}{2}$(x+2)(x-6)的对称轴是( )
| A. | 直线x=-2 | B. | 直线x=6 | C. | 直线x=2 | D. | 直线x=4 |