题目内容
7.已知(2a-1)2+|b+1|=0,求($\frac{1}{a}$)2+($\frac{1}{b}$)2016.分析 根据非负数的和为零,可得每个非负数同时为零,根据负数的偶数次幂是正数,可得答案.
解答 解:由(2a-1)2+|b+1|=0,得
2a-1=0,b+1=0.
解得a=$\frac{1}{2}$,b=-1.
($\frac{1}{a}$)2+($\frac{1}{b}$)2016=22+(-1)2016=4+1=5.
点评 本题考查了非负数的性质,利用非负数的和为零得出每个非负数同时为零是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
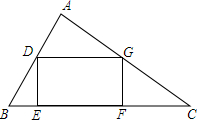 如图,已知△ABC中,BC=24,在△ABC中截出一个矩形DEFG,已知矩形的面积S与EF的长x满足关系式:S=-$\frac{2}{3}$x2+16x,问:EF的长为多少时,矩形的面积等于72?
如图,已知△ABC中,BC=24,在△ABC中截出一个矩形DEFG,已知矩形的面积S与EF的长x满足关系式:S=-$\frac{2}{3}$x2+16x,问:EF的长为多少时,矩形的面积等于72? 如图,在边长为1的网格中有一个平面直角坐标系.
如图,在边长为1的网格中有一个平面直角坐标系. 如图,已知AD平分∠BAC,∠BAC+∠BDC=180°.
如图,已知AD平分∠BAC,∠BAC+∠BDC=180°.