题目内容
3.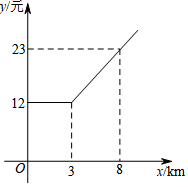 为了追求更舒适的出行体验,利用网络呼出专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用y(元)与行驶里程x(km)的函数关系如图所示,请根据图象解答下列问题:
为了追求更舒适的出行体验,利用网络呼出专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用y(元)与行驶里程x(km)的函数关系如图所示,请根据图象解答下列问题:(1)求y与x之间的函数关系式.
(2)若专车低速行驶(时速≥12km/h),每分钟另加0.4元的低速费(不足1分钟的部分按1分钟计算).某乘客有一次在非高峰期乘坐专车,途中低速行驶了6分钟,共付费32元,求这位乘客乘坐专车的行驶里程.
分析 (1)找出函数图象上点的坐标,利用待定系数法即可求出y与x之间的函数关系式;
(2)代入y=32-0.4×6,求出x值即可.
解答 解:(1)设y与x之间的函数关系式为y=kx+b.
当0<x≤3时,y=12;
当x≥3时,将(3,12)、(8,23)代入y=kx+b,
$\left\{\begin{array}{l}{3k+b=12}\\{8k+b=23}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2.2}\\{b=5.4}\end{array}\right.$,
∴此时y=2.2x+5.4.
综上所述:y与x之间的函数关系式为y=$\left\{\begin{array}{l}{12(0≤x≤3)}\\{2.2x+5.4(x≥3)}\end{array}\right.$.
(2)当y=2.2x+5.4=32-0.4×6时,x=11.
答:这位乘客乘坐专车的行驶里程为11千米.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:(1)根据图象上点的坐标利用待定系数法求出函数关系式;(2)代入y=32-0.4×6,求出与之对应的x值.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
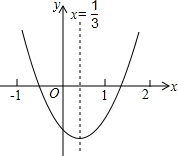 从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )
从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )
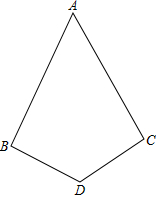 如图已知:AB=AC.DB=DC,∠ABD=∠ACD.试判断直线AD、BC的位置关系并加以证明.
如图已知:AB=AC.DB=DC,∠ABD=∠ACD.试判断直线AD、BC的位置关系并加以证明. 如图,点P是⊙O上一点,请用尺规过点P作⊙O的切线(不写画法,保留作图痕迹).
如图,点P是⊙O上一点,请用尺规过点P作⊙O的切线(不写画法,保留作图痕迹).