题目内容
5．函数y=1+$\sqrt{x+3}$中自变量x的取值范围是x≥-3．分析 本题主要考查自变量的取值范围，函数关系中主要有二次根式．根据二次根式的意义，被开方数是非负数．
解答 解：根据题意得：x+3≥0，
解得x≥-3．
故答案为x≥-3．
点评 本题考查了函数自变量的取值范围问题，函数自变量的范围一般从三个方面考虑：
（1）当函数表达式是整式时，自变量可取全体实数；
（2）当函数表达式是分式时，考虑分式的分母不能为0；
（3）当函数表达式是二次根式时，被开方数为非负数．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
5．若△ABC∽△DEF，则AC=5，DF=1.5，则△ABC∽△DEF的相似比为（ ）
| A． | $\frac{3}{10}$ | B． | $\frac{10}{3}$ | C． | $\frac{7}{10}$ | D． | $\frac{10}{7}$ |
10．下列各组运算中，结果为负数的是（ ）
| A． | -（-3） | B． | |-3| | C． | 3×（-2）2 | D． | -32 |
17．计算（$\sqrt{3}$）2-1的结果是（ ）
| A． | -2 | B． | 2 | C． | 2$\sqrt{3}$ | D． | 2$\sqrt{3}$-1 |
14．下列等式错误的是（ ）
| A． | $\sqrt{{{（-2）}^2}}=2$ | B． | $\root{3}{{{{（{-2}）}^3}}}=-2$ | C． | $\sqrt{\frac{1}{2}}=\frac{{\sqrt{2}}}{2}$ | D． | $\sqrt{（-3）×（{-2}）}=\sqrt{-3}×\sqrt{-2}$ |
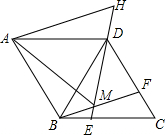如图，在菱形ABCD中，AB=BD，点E、F分别在BC、CD上，且BE=CF，连接BF、DE交于点M，延长DE到H使DE=BM，连接AM、AH．则以下四个结论：①△BDF≌△DCE；②∠BMD=120°；③△AMH是等边三角形；其中正确结论的个数是（ ）