题目内容
7. 如图,一段抛物线:y=-(x-1)2+1(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;如此进行下去,直至得到C8,若点P(14.5,m)在抛物线C8上,则m的值为-$\frac{3}{4}$.
如图,一段抛物线:y=-(x-1)2+1(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;如此进行下去,直至得到C8,若点P(14.5,m)在抛物线C8上,则m的值为-$\frac{3}{4}$.
分析 求出抛物线C1与x轴的交点坐标,观察图形可知第奇数号抛物线都在x轴上方、第偶数号抛物线都在x轴下方,再根据向右平移横坐标相加表示出抛物线C8的解析式,然后把点P的横坐标代入计算即可得解.
解答 解:抛物线C1:y=-(x-1)2+1=-x(x-2)与x轴的交点为(0,0)、(2,0),
将C1绕A1旋转180°得到C2,则C2的解析式为y=(x-2)(x-4),
同理可得C3的解析式为y=-(x-4)(x-6),
C4的解析式为y=(x-6)(x-8),
C5的解析式为y=-(x-8)(x-10),
C6的解析式为y=(x-10)(x-12),
C7的解析式为y=-(x-12)(x-14),
C8的解析式为y=(x-14)(x-16),
∵点P(14.5,m)在抛物线C8上,
∴m=(14.5-14)×(14.5-16)=-$\frac{3}{4}$,
故答案为:-$\frac{3}{4}$.
点评 本题考查了二次函数图象与几何变换,根据平移规律得出C8与x轴的交点坐标,进而得到解析式是解题关键.

练习册系列答案
相关题目
15.某公司销售一组共有10名员工,每月所创利润如下表所示:
则这个销售小组每人所创月利润平均是2.3万元.
| 月利润(万元) | 1 | 2 | 3 | 4 |
| 人数 | 2 | 4 | 3 | 1 |

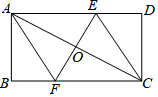 如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.
如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.