题目内容
12.点A,B分别是双曲线y=$\frac{k}{x}$(k>0)上的点,AC⊥y轴正半轴于点C,BD⊥y轴于点D,联结AD,BC,若四边形ACBD是面积为12的平行四边形,则k=6.分析 先根据四边形ACBD为平行四边形的性质和反比例函数的对称性得到A点与点B关于原点对称,然后根据平行四边形的性质和k的几何意义求解.
解答  解:∵点A,B分别是双曲线y=$\frac{k}{x}$(k>0)上的点,AC⊥y轴正半轴于点C,BD⊥y轴于点D,
解:∵点A,B分别是双曲线y=$\frac{k}{x}$(k>0)上的点,AC⊥y轴正半轴于点C,BD⊥y轴于点D,
∴AC∥BD,
∵四边形ACBD是面积为12的平行四边形,
∴AC=BD,
∴A点与点B关于原点对称,
∴OA=OB,OC=OD,
∴S四边形ACBD=4S△AOC=12,
∴S△AOC=3,
∴k=6,
故答案为:6.
点评 本题考查了反比例函数系数k的几何意义,平行四边形的性质,正确的理解题意是解题的关键.

练习册系列答案
相关题目
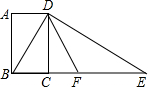 如图所示,四边形ABCD是矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=5,设AB=x,AD=y,则x2+(y-5)2的值为25.
如图所示,四边形ABCD是矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=5,设AB=x,AD=y,则x2+(y-5)2的值为25. 如图,一段抛物线:y=-(x-1)2+1(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;如此进行下去,直至得到C8,若点P(14.5,m)在抛物线C8上,则m的值为-$\frac{3}{4}$.
如图,一段抛物线:y=-(x-1)2+1(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;如此进行下去,直至得到C8,若点P(14.5,m)在抛物线C8上,则m的值为-$\frac{3}{4}$.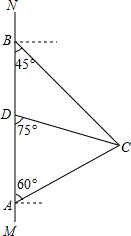 如图,在南北方向的海岸线MN上,有A,B两艘巡逻船,现均收到故障船C的求救信号,已知A,B两船相距100($\sqrt{3}$+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A,B两艘巡逻船,现均收到故障船C的求救信号,已知A,B两船相距100($\sqrt{3}$+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.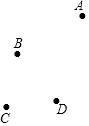 如题,平面上四个点A,B,C,D,按要求完成下列问题:
如题,平面上四个点A,B,C,D,按要求完成下列问题: 如图,已知△ABC,用尺规作出△ABC外心.(保留作图痕迹,不写作法)
如图,已知△ABC,用尺规作出△ABC外心.(保留作图痕迹,不写作法)