题目内容
19．（1）解方程：$\frac{x-1}{x-2}$-$\frac{1}{2-x}$=3；（2）解不等式组：$\left\{\begin{array}{l}{5x-2＞3（x+1）}\\{\frac{x}{2}-1≤7-\frac{3}{2}x}\end{array}\right.$．
分析 （1）解分式方程的步骤：①去分母；②求出整式方程的解；③检验；④得出结论．
（2）解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分．
解答 解：（1）整理得，
$\frac{x-1}{x-2}+\frac{1}{x-2}=3$
去分母得，
x-1+1=3（x-2）
解得x=$\frac{5}{2}$
经检验，x=$\frac{5}{2}$是原方程的解；
（2）$\left\{\begin{array}{l}{5x-2＞3（x+1）①}\\{\frac{x}{2}-1≤7-\frac{3}{2}x②}\end{array}\right.$
解不等式①，得$x＞\frac{5}{2}$
解不等式②，得x≤4
∴不等式组的解集为$\frac{5}{2}$＜x≤4
点评 本题主要考查了解分式方程以及解一元一次不等式，解题时注意：解分式方程时，一定要检验．解集的规律为：同大取大；同小取小；大小小大中间找；大大小小找不到．
练习册系列答案
相关题目
9．为了调查居民的生活水平，有关部门对某居委会的50户居民的家庭存款额进行了调查，数据（单位：万元）如下：
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
（1）这50个家庭存款额的最大值、最小值分别是多少？它们相差多少？
（2）填表：
（3）根据上表谈谈这50户家庭存款额的分布情况．
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
（1）这50个家庭存款额的最大值、最小值分别是多少？它们相差多少？
（2）填表：
| 存款额x（万元） | 划记 | 户数 |
| 1.0≤x＜2.0 | 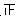 | 4 |
| 2.0≤x＜3.0 | 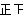 | 8 |
| 3.0≤x＜4.0 | 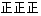 | 15 |
| 4.0≤x＜5.0 | 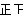 | 8 |
| 5.0≤x＜6.0 |  | 10 |
| 6.0≤x＜7.0 |  | 3 |
| 7.0≤x＜8.0 |  | 2 |
10．用棋子摆出下列一组图形，请观察图形，根据你发现的规律解答下列问题：
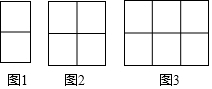
（1）填写下表：
（2）第n个图形中共有3n+3枚棋子；
（3）照这样的方式摆下去，第100个图形中棋子数是多少枚？
（1）填写下表：
| 图形编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 图形中棋子的枚数 | 6 | 9 | 12 | 15 | 18 | 21 |
（3）照这样的方式摆下去，第100个图形中棋子数是多少枚？
如图，一段抛物线：y=-（x-1）2+1（0≤x≤2）记为C1，它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；如此进行下去，直至得到C8，若点P（14.5，m）在抛物线C8上，则m的值为-$\frac{3}{4}$．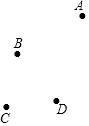
如题，平面上四个点A，B，C，D，按要求完成下列问题：
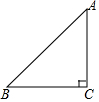如图，△ABC是等腰直角三角形，∠C=90°．
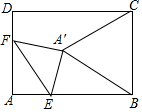如图，在矩形ABCD中，AB=8，AD=6，点E为AB上一点，AE=2$\sqrt{3}$，点F在AD上，将△AEF沿EF折叠，当折叠后点A的对应点A′恰好落在BC的垂直平分线上时，折痕EF的长为4或4$\sqrt{3}$．