题目内容
15.用公式法解一元二次方程:(1)x2+4x-3=0
(2)p${\;}^{2}+3=2\sqrt{3}$p.
分析 (1)先计算出判别式的值,然后利用求根公式求解;
(2)先把方程化为一般式,然后利用求根公式法解方程.
解答 解:(1)△=42-4×(-3)=28,
x=$\frac{-4±2\sqrt{7}}{2}$=-2±$\sqrt{7}$
所以x1=-2+$\sqrt{7}$,x2=-2-$\sqrt{7}$;
(2)p2-2$\sqrt{3}$p+3=0,
△=(2$\sqrt{3}$)2-4×3=0,
p=$\frac{2\sqrt{3}±0}{2}$=$\sqrt{3}$
所以p1=p2=$\sqrt{3}$.
点评 本题考查了解一元二次方程-公式法:用求根公式解一元二次方程的方法是公式法.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
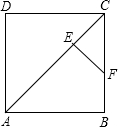 已知:如图,E是正方形ABCD对角线AC上一点,且AE=AB,EF⊥AC,交BC于F.求证:BF=EC.
已知:如图,E是正方形ABCD对角线AC上一点,且AE=AB,EF⊥AC,交BC于F.求证:BF=EC.