题目内容
10.直角梯形ABCD中,上底为3,一个下底角为30°,斜腰长等于4,则梯形的面积为6+2$\sqrt{3}$.分析 作出图形,过点A作AE⊥BC于E,可得四边形AECD是矩形,可求出CE的长,再求出BE的长,根据梯形的面积公式计算即可.
解答 解:如图,过点A作AE⊥BC于E,
∵梯形ABCD是直角梯形,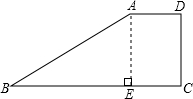
∴四边形AECD是矩形,
∴AD=CE=3,
∵∠B=30°,AB=4,
∴AE=2,
∴BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=2$\sqrt{3}$,
∴BC=BE+CE=3+2$\sqrt{3}$,
∴则梯形的面积=$\frac{(AD+BC)•AE}{2}$=$\frac{(6+2\sqrt{3})×2}{2}$=6+2$\sqrt{3}$
故答案为:6+2$\sqrt{3}$.
点评 本题考查了直角梯形的性质,根据直角三角形30°角所对的直角边等于斜边的一半,作辅助线构造出直角三角形与矩形是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
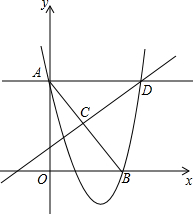 如图,点B是x轴上一动点,点A(0,2),过A作x轴的平行线交AB的中垂线CD于D,点C为垂足,抛物线y=ax2+bx+c经过A,B,D三点,当点B从(1,0)运动到(4,0)时,则a的变化范围是a≤-$\frac{1}{3}$或a≥$\frac{4}{3}$.
如图,点B是x轴上一动点,点A(0,2),过A作x轴的平行线交AB的中垂线CD于D,点C为垂足,抛物线y=ax2+bx+c经过A,B,D三点,当点B从(1,0)运动到(4,0)时,则a的变化范围是a≤-$\frac{1}{3}$或a≥$\frac{4}{3}$.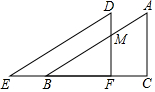 如图,将直角△ABC沿着射线CB的方向平移到△DEF的位置.已知AC=8,DM=3,平移的距离为6,求四边形DEBM的面积.
如图,将直角△ABC沿着射线CB的方向平移到△DEF的位置.已知AC=8,DM=3,平移的距离为6,求四边形DEBM的面积.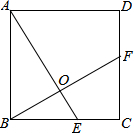 如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF.
如图,正方形ABCD中,E、F分别是AB、BC边上的点,且AE=BF.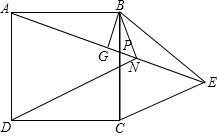 如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在点AP延长线上取点E.使AG=GE.连接BE、CE.
如图,P为正方形ABCD边BC上任一点,BG⊥AP于点G,在点AP延长线上取点E.使AG=GE.连接BE、CE.