题目内容
5.用适当的方法解下列一元二次方程.(1)(2x+1)2=3(2x+1)
(2)(x+1)(2x-3)=1.
分析 (1)先移项得(2x+1)2-3(2x+1)=0,然后利用因式分解法解方程;
(2)先把方程化为一般式,然后利用求根公式法解方程.
解答 解:(1)(2x+1)2-3(2x+1)=0,
(2x+1)(2x+1-3)=0,
2x+1=0或2x+1-3=0,
所以x1=-$\frac{1}{2}$,x2=1;
(2)方程化为2x2-x-4=0,
△=(-1)2-4×2×(-4)=33,
x=$\frac{1±\sqrt{33}}{2×2}$,
所以x1=$\frac{1+\sqrt{33}}{4}$,x2=$\frac{1-\sqrt{33}}{4}$.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了公式法解一元二次方程.

练习册系列答案
相关题目
17.如图,是一组按照某种程度摆放成的图案,则图6中三角形的个数是( )

| A. | 18 | B. | 19 | C. | 20 | D. | 21 |
 如图,在平面直角坐标系中,点A(2,2)在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )
如图,在平面直角坐标系中,点A(2,2)在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有( )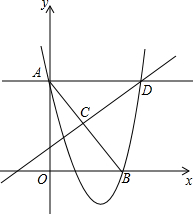 如图,点B是x轴上一动点,点A(0,2),过A作x轴的平行线交AB的中垂线CD于D,点C为垂足,抛物线y=ax2+bx+c经过A,B,D三点,当点B从(1,0)运动到(4,0)时,则a的变化范围是a≤-$\frac{1}{3}$或a≥$\frac{4}{3}$.
如图,点B是x轴上一动点,点A(0,2),过A作x轴的平行线交AB的中垂线CD于D,点C为垂足,抛物线y=ax2+bx+c经过A,B,D三点,当点B从(1,0)运动到(4,0)时,则a的变化范围是a≤-$\frac{1}{3}$或a≥$\frac{4}{3}$.
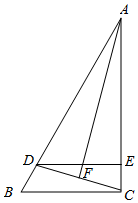 如图,在△ABC中,∠ACB=90°.D为AB上一点,且AC=AD.连接CD,过点D作DE∥BC.DE与AC相交于E.F为CD的中点,连接AF,EF.
如图,在△ABC中,∠ACB=90°.D为AB上一点,且AC=AD.连接CD,过点D作DE∥BC.DE与AC相交于E.F为CD的中点,连接AF,EF.