题目内容
14.关于x的方程$\frac{x-a}{bc}$+$\frac{x-b}{ac}$+$\frac{x-c}{ab}$=2($\frac{1}{a}$+$\frac{1}{b}$+1$\frac{1}{c}$),其中a+b+c≠0,方程的解为x=a+b+c.分析 首先去分母,进而利用完全平方公式化简求值即可.
解答 解:方程两边同乘以abc,得:
a(x-a)+b(x-b)+c(x-c)=2(bc+ac+ab)
ax+bx+cx=a2+b2+c2+2bc+2ac+2ab
(a+b+c)x=(a+b+c)2,
整理得出:x=a+b+c,
故答案为:x=a+b+c.
点评 此题主要考查了解分式方程,掌握解分式方程的基本步骤是基础,正确化简是解题关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
8.不等式组$\left\{\begin{array}{l}{\frac{3x-1}{2}>2-x}\\{8-4x≤0}\end{array}\right.$的解集在数轴上可表示为( )
| A. |  | B. | 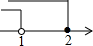 | C. |  | D. |  |
9.有三张正面分别写有数字-1,1,2的卡片,它们的材质、大小和背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后再从剩余的两张卡片随机抽取一张,以其正面的数学作为b的值,则满足a2+b2=5的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
6.在下列命题中,是真命题的为( )
| A. | 对角线垂直的四边形是菱形 | |
| B. | 对角线垂直且相等的四边形是正方形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
3.使式子$\sqrt{\frac{1}{x+1}}$有意义的x取值范围是( )
| A. | x>-1 | B. | x≥-1 | C. | x<-1 | D. | x≤-1 |
4.有一组数据:11、9、13、x、15,它们的平均数是16,则这组数据的中位数是( )
| A. | 11 | B. | 13 | C. | 15 | D. | 17 |