题目内容
17.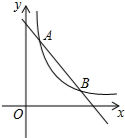 如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.(1)求反比例函数的表达式及点B的坐标;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.
分析 (1)把点A(1,a)代入一次函数y=-x+5,即可得出a,再把点A坐标代反比例函数y=$\frac{k}{x}$,即可得出k,两个函数解析式联立求得点B坐标;
(2)作点B作关于y轴的对称点D,连接AD,交y轴于点P,此时PA+PB的值最小,求出直线AD的解析式,令x=0,即可得出点P坐标.
解答 解:(1)把点A(1,a)代入一次函数y=-x+5,
得a=-1+5,
解得a=4,
∴A(1,4),
点A(1,4)代入反比例函数y=$\frac{k}{x}$,
得k=4,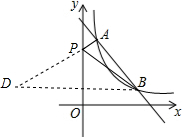
∴反比例函数的表达式y=$\frac{4}{x}$,
两个函数解析式联立列方程组得$\left\{\begin{array}{l}{y=-x+5}\\{y=\frac{4}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$
∴点B坐标(4,1);
(2)作点B作关于y轴的对称点D(-4,1),连接AD,交y轴于点P,此时PA+PB的值最小,
设直线AD的解析式为y=mx+n,
把A,D两点代入得,$\left\{\begin{array}{l}{m+n=4}\\{-4m+n=1}\end{array}\right.$,
解得m=$\frac{3}{5}$,n=$\frac{17}{5}$,
∴直线AD的解析式为y=$\frac{3}{5}$x+$\frac{17}{5}$,
令x=0,得y=$\frac{17}{5}$,
∴点P坐标(0,$\frac{17}{5}$).
点评 本题考查了一次函数和反比例函数的交点问题以及轴对称-最短路线问题,利用了待定系数法求解析式,两点之间线段最短的性质.

| A. | 三点确定一个圆 | |
| B. | 平分弦的直径垂直于弦,并且平分弦所对的两条弧 | |
| C. | 与直径垂直的直线是圆的切线 | |
| D. | 能够互相重合的弧是等弧 |
 如图,在平面直角坐标系xOy中,点A的坐标为(-1,2),AB⊥x轴于点B.以原点O为位似中心,将△OAB放大为原来的2倍,得到△OA1B1,且点A1在第二象限,则点A1的坐标为( )
如图,在平面直角坐标系xOy中,点A的坐标为(-1,2),AB⊥x轴于点B.以原点O为位似中心,将△OAB放大为原来的2倍,得到△OA1B1,且点A1在第二象限,则点A1的坐标为( )| A. | (-2,4) | B. | ($-\frac{1}{2}$,1) | C. | (2,-4) | D. | (2,4) |
 如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:$\sqrt{3}$≈1.7)
如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:$\sqrt{3}$≈1.7) 如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.
如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.