题目内容
19.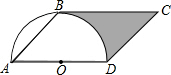 如图,已知?ABCD,∠A=45°,AD=4,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积为6-π(结果保留π).
如图,已知?ABCD,∠A=45°,AD=4,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积为6-π(结果保留π).
分析 连接OB,求出OB=OA=OD=$\frac{1}{2}$AD=2,由S阴影部分=S?ABCD-SRt△AOB-S扇形BOD即可得出结果.
解答 解:连接OB,如图所示: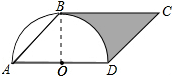
∵半圆O与BC相切于点B,
∴OB⊥BC,
∵四边形ABCD为平行四边形,
∴BO⊥AD,
∵AD=4,
∴OB=OA=OD=$\frac{1}{2}$AD=2,
∴S阴影部分=S?ABCD-SRt△AOB-S扇形BOD
=4×2-$\frac{1}{2}$×2×2-$\frac{1}{4}π$×22
=6-π.
故答案为:6-π.
点评 此题考查了平行四边形的性质、切线的性质、平行四边形面积与三角形面积以及扇形面积的计算等知识;把不规则图形的面积转化为规则图形的面积是解决问题的关键.

练习册系列答案
相关题目
8.下表是二次函数y=ax2+bx+c( a≠0)图象上部分点的横坐标(x)和纵坐标(y).
(1)观察表格,直接写出m=3;
(2)其中A(x1,y1)、B(x2,y2)在函数的图象上,且-1<x1<0,2<x2<3,则y1>y2(用“>”或“<”填空);
(3)求这个二次函数的表达式.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | m | 8 | … |
(2)其中A(x1,y1)、B(x2,y2)在函数的图象上,且-1<x1<0,2<x2<3,则y1>y2(用“>”或“<”填空);
(3)求这个二次函数的表达式.
 如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:$\sqrt{3}$≈1.7)
如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:$\sqrt{3}$≈1.7)
 请你根据如图所示已知条件,推想正确结论,要求每个结论同时含有字母a,b.写出至少三条正确结论:b>a,ab>0,a+b<0.
请你根据如图所示已知条件,推想正确结论,要求每个结论同时含有字母a,b.写出至少三条正确结论:b>a,ab>0,a+b<0.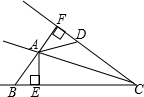 如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F.
如图,AC平分∠BCD,AB=AD,AE⊥BC于E,AF⊥CD于F. 如图,P为等边△ABC内一点,PA=2,PB=1,PC=$\sqrt{3}$,则△ABC的面积为$\frac{7\sqrt{3}}{4}$.
如图,P为等边△ABC内一点,PA=2,PB=1,PC=$\sqrt{3}$,则△ABC的面积为$\frac{7\sqrt{3}}{4}$.