题目内容
18.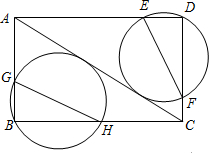 如图,在矩形ABCD中,BC=5,AB=3,分别经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是$\frac{15\sqrt{34}}{17}$.
如图,在矩形ABCD中,BC=5,AB=3,分别经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是$\frac{15\sqrt{34}}{17}$.
分析 如图,设GH的中点为O,过O点作OM⊥AC,过B点作BN⊥AC,垂足分别为M、N,根据∠B=90°可知,点O为过B点的圆的圆心,OM为⊙O的半径,BO+OM为直径,可知BO+OM≥BN,故当BN为直径时,直径的值最小,即直径GH也最小,同理可得EF的最小值.
解答 解:如图,设GH的中点为O,
过O点作OM⊥AC,过B点作BN⊥AC,垂足分别为M、N,
在Rt△ABC中,BC=5,AB=3,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{34}$,
由面积法可知,BN•AC=AB•BC,
解得BN=$\frac{15}{\sqrt{34}}$,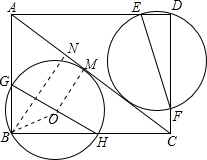
∵∠B=90°,
∴GH为⊙O的直径,点O为过B点的圆的圆心,
∵⊙O与AC相切,
∴OM为⊙O的半径,
∴BO+OM为直径,
又∵BO+OM≥BN,
∴当BN为直径时,直径的值最小,
此时,直径GH=BN=$\frac{15}{\sqrt{34}}$,
同理可得:EF的最小值为$\frac{15}{\sqrt{34}}$,
∴EF+GH的最小值是$\frac{30\sqrt{34}}{34}$=$\frac{15\sqrt{34}}{17}$.
故答案为:$\frac{15\sqrt{34}}{17}$.
点评 本题考查了切线的性质,垂线的性质及勾股定理的运用.关键是明确EF、GH为两圆的直径,根据题意确定直径的最小值.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
9.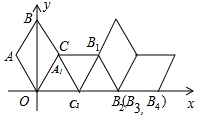 如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1,A2,A3,…,则A2015的坐标为.( )
如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1,A2,A3,…,则A2015的坐标为.( )
 如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1,A2,A3,…,则A2015的坐标为.( )
如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1,A2,A3,…,则A2015的坐标为.( )| A. | (1343,0) | B. | (1347,0) | C. | (1343$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | D. | (1347$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) |
13.下列各选项的图形中,中心对称图形是( )
| A. |  | B. |  | C. | 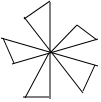 | D. | 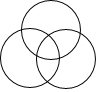 |
10.已知点M(1-2m,m-1)在第四象限内,那么m的取值范围是( )
| A. | m>1 | B. | m<$\frac{1}{2}$ | C. | $\frac{1}{2}$<m<1 | D. | m<$\frac{1}{2}$或m>1 |
7.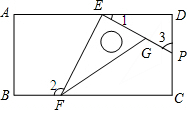 如图,一个含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠3=65°,那么∠2的度数是( )
如图,一个含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠3=65°,那么∠2的度数是( )
 如图,一个含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠3=65°,那么∠2的度数是( )
如图,一个含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠3=65°,那么∠2的度数是( )| A. | 100° | B. | 105° | C. | 115° | D. | 120° |
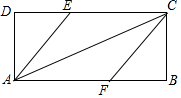 矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.∠ECA=∠FCA.
矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.∠ECA=∠FCA.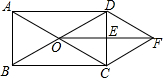 如图所示,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证:
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证: 把一副常用的三角尺按如图所示的方式拼在一起,则∠ABC=75°.
把一副常用的三角尺按如图所示的方式拼在一起,则∠ABC=75°.