题目内容
9.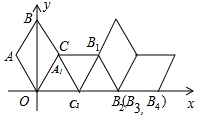 如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1,A2,A3,…,则A2015的坐标为.( )
如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点A的落点依次为A1,A2,A3,…,则A2015的坐标为.( )| A. | (1343,0) | B. | (1347,0) | C. | (1343$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | D. | (1347$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) |
分析 连接AC,根据条件可以求出AC,由第5次、第6次、第7次翻转后的图形,容易发现规律:每翻转6次,图形向右平移4.由于2015=335×6+5,因此点A5向右平移1340(即335×4)即可到达点A2015,根据点A5的坐标就可求出点A2015的坐标.
解答 解:连接AC,如图所示.
∵四边形OABC是菱形,
∴OA=AB=BC=OC.
∵∠ABC=60°,
∴△ABC是等边三角形.
∴AC=AB.
∴AC=OA.
∵OA=1,
∴AC=1.
根据第5次、第6次、第7次翻转后的图形.
由图可知:每翻转6次,图形向右平移4.
∵2015=335×6+5,
∴点A5向右平移1340(即335×4)到点A2014.
∵A5的坐标为(3,0),
∴A2014的坐标为(3+1340,0),
∴A2015的坐标为(1343,0).
点评 本题考查了菱形的性质、等边三角形的判定与性质等知识,考查了操作、探究、发现规律的能力.发现“每翻转6次,图形向右平移4”是解决本题的关键.

练习册系列答案
相关题目
17. 如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC,则∠B为( )
如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC,则∠B为( )
 如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC,则∠B为( )
如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC,则∠B为( )| A. | 80° | B. | 95° | C. | 110° | D. | 105° |
4.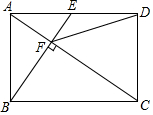 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;正确的是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
1.下列说法中错误的是( )
| A. | 原点的坐标是(0,0) | B. | x轴上的所有点的纵坐标都相等 | ||
| C. | y轴上的所有点的横坐标都相等 | D. | 点(0,-1)在第四象限 |
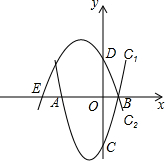 已知抛物线C1:y=x2+2x-3与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线C2:y=ax2+bx+c经过点B,与x轴的另一个交点为E(-4,0),与y轴交于点D(0,2).
已知抛物线C1:y=x2+2x-3与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线C2:y=ax2+bx+c经过点B,与x轴的另一个交点为E(-4,0),与y轴交于点D(0,2).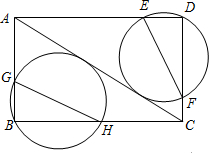 如图,在矩形ABCD中,BC=5,AB=3,分别经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是$\frac{15\sqrt{34}}{17}$.
如图,在矩形ABCD中,BC=5,AB=3,分别经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是$\frac{15\sqrt{34}}{17}$.