题目内容
6.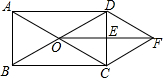 如图所示,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证:
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证:(1)OD=CF;
(2)四边形ODFC是菱形.
分析 (1)欲证明OD=CF,只要证明△ODE≌△FCE(ASA)即可.
(2)首先证明四边形ODFC是平行四边形,再由OD=OC即可推出四边形ODFC是菱形.
解答 证明:(1)∵CF∥BD,
∴∠DOE=∠CFE,
∵E是CD的中点,
∴CE=DE
在△ODE和△FCE中,
$\left\{\begin{array}{l}∠DOE=∠CFE\\ CE=DE\\∠DEO=∠CEF\end{array}\right.$,
∴△ODE≌△FCE(ASA)
∴OD=CF.
(2)由(1)知OD=CF,
∵CF∥BD,
∴四边形ODFC是平行四边形
在矩形ABCD中,OC=OD,
∴四边形ODFC是菱形.
点评 本题考查矩形的性质、全等三角形的判定和性质、菱形的判定等知识,解题的关键是正确寻找全等三角形,记住矩形、菱形的判定方法,属于中考常考题型.

练习册系列答案
相关题目
17. 如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC,则∠B为( )
如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC,则∠B为( )
 如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC,则∠B为( )
如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折得△FMN,若MF∥AD,FN∥DC,则∠B为( )| A. | 80° | B. | 95° | C. | 110° | D. | 105° |
1.下列说法中错误的是( )
| A. | 原点的坐标是(0,0) | B. | x轴上的所有点的纵坐标都相等 | ||
| C. | y轴上的所有点的横坐标都相等 | D. | 点(0,-1)在第四象限 |
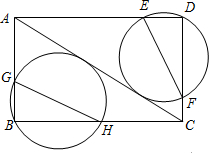 如图,在矩形ABCD中,BC=5,AB=3,分别经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是$\frac{15\sqrt{34}}{17}$.
如图,在矩形ABCD中,BC=5,AB=3,分别经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是$\frac{15\sqrt{34}}{17}$.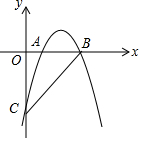 已知抛物线y=-x2+4x-3经过A(1,0),B(3,0),点C(0,-3),在抛物线上是否存在一点P,使得∠PCB>∠ACB,若存在,求出P点的横坐标的取值范围.
已知抛物线y=-x2+4x-3经过A(1,0),B(3,0),点C(0,-3),在抛物线上是否存在一点P,使得∠PCB>∠ACB,若存在,求出P点的横坐标的取值范围.