题目内容
 学着说点理.
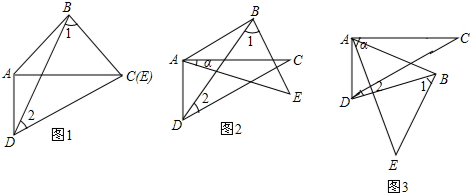
学着说点理.(1)如图1:∠1=∠2=∠3,完成说理过程并注明理由:
(1)∵∠1=∠2
∴
(2)∵∠1=∠3
∴
(2)已知:如图2,AB∥CD,∠A=∠D,试说明AC∥DE成立的理由.下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.
证明:∵AB∥CD (已知)
∴∠A=
又∵∠A=∠D
∴∠
∴AC∥DE
考点:平行线的判定与性质
专题:推理填空题
分析:(1)根据同位角相等,两直线平行肯定判断EF∥CD;由∠1=∠3,根据内错角相等,两直线平行可得到AB∥CD;
(2)根据平行线的性质由AB∥CD得到∠A=∠ACD,加上∠A=∠D,根据等量代换得∠ACD=∠D,然后根据平行线的判定得到AC∥DE.
(2)根据平行线的性质由AB∥CD得到∠A=∠ACD,加上∠A=∠D,根据等量代换得∠ACD=∠D,然后根据平行线的判定得到AC∥DE.
解答:解:(1)如图1:∠1=∠2=∠3,完成说理过程并注明理由:
(1)∵∠1=∠2
∴EF∥BD;
(2)∵∠1=∠3
∴AB∥CD;
(2)已知:如图2,AB∥CD,∠A=∠D,试说明AC∥DE成立的理由.下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.
证明:∵AB∥CD,
∴∠A=∠ACD,
又∵∠A=∠D,
∴∠ACD=∠D,
∴AC∥DE.
故答案为EF,BD,AB,CD;∠ACD,已知,∠ACD,∠D,内错角相等,两直线平行.
(1)∵∠1=∠2
∴EF∥BD;
(2)∵∠1=∠3
∴AB∥CD;
(2)已知:如图2,AB∥CD,∠A=∠D,试说明AC∥DE成立的理由.下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.
证明:∵AB∥CD,
∴∠A=∠ACD,
又∵∠A=∠D,
∴∠ACD=∠D,
∴AC∥DE.
故答案为EF,BD,AB,CD;∠ACD,已知,∠ACD,∠D,内错角相等,两直线平行.
点评:本题考查了平行线的判定与性质:同位角相等,两直线平行;同旁内角互补,两直线平行;内错角相等,两直线平行.两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
下列调查中,适宜采用全面调查方式的是( )
| A、调查乘坐飞机的旅客是否携带了违禁物品 |
| B、了解南通市中学生的视力情况 |
| C、调查南通市场上酸奶的质量情况 |
| D、了解南通市中学生课外阅读的情况 |

 已知:如图,AD⊥BC,EF⊥BC,∠1=∠2.求证:∠DGC=∠BAC.
已知:如图,AD⊥BC,EF⊥BC,∠1=∠2.求证:∠DGC=∠BAC. 如图:
如图: