题目内容
9. 如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为24.
如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为24.
分析 由菱形的性质可得出AC⊥BD,AB=BC=CD=DA,再根据直角三角形斜边上的中线等于斜边的一半得出AD的长,结合菱形的周长公式即可得出结论.
解答 解:∵四边形ABCD为菱形,
∴AC⊥BD,AB=BC=CD=DA,
∴△AOD为直角三角形.
∵OE=3,且点E为线段AD的中点,
∴AD=2OE=6.
C菱形ABCD=4AD=4×6=24.
故答案为:24.
点评 本题考查了菱形的性质以及直角三角形的性质,解题的关键是求出AD=6.本题属于基础题,难度不大,解决该题型题目时,根据菱形的性质找出对角线互相垂直,再通过直角三角形的性质找出菱形的一条变成是关键.

练习册系列答案
相关题目
17. 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为( )
如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为( )
 如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为( )
如图,热气球的探测器显示,从热气球A处看一栋楼顶部B处的仰角为30°,看这栋楼底部C处的俯角为60°,热气球A处与楼的水平距离为120m,则这栋楼的高度为( )| A. | 160$\sqrt{3}$m | B. | 120$\sqrt{3}$m | C. | 300m | D. | 160$\sqrt{2}$m |
14.下列根式中是最简二次根式的是( )
| A. | $\sqrt{\frac{2}{3}}$ | B. | $\sqrt{3}$ | C. | $\sqrt{9}$ | D. | $\sqrt{12}$ |
18.下列实数中,是无理数的为( )
| A. | -4 | B. | 0.101001 | C. | $\frac{1}{3}$ | D. | $\sqrt{2}$ |
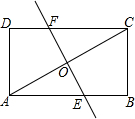 如图,矩形ABCD中,对角线AC的中点为O,过O作EF⊥AC,分别交AB、DC于E、F,若AB=4,BC=2,那么线段EF的长为$\sqrt{5}$.
如图,矩形ABCD中,对角线AC的中点为O,过O作EF⊥AC,分别交AB、DC于E、F,若AB=4,BC=2,那么线段EF的长为$\sqrt{5}$.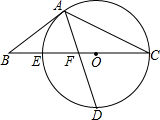 如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF. 将一张矩形纸片折叠成如图所示的图形,若AB=6cm,则AC=6cm.
将一张矩形纸片折叠成如图所示的图形,若AB=6cm,则AC=6cm.