题目内容
20.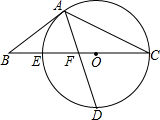 如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=$\sqrt{10}$,求⊙O的半径r及sinB.
分析 (1)连接OA、OD,如图,根据垂径定理得OD⊥BC,则∠D+∠OFD=90°,再由AB=BF,OA=OD得到∠BAF=∠BFA,∠OAD=∠D,加上∠BFA=∠OFD,所以∠OAD+∠BAF=90°,则OA⊥AB,然后根据切线的判定定理即可得到AB是⊙O切线;
(2)先表示出OF=4-r,OD=r,在Rt△DOF中利用勾股定理得r2+(4-r)2=($\sqrt{10}$)2,解方程得到r的值,那么OA=3,OF=CF-OC=4-3=1,BO=BF+FO=AB+1.
然后在Rt△AOB中利用勾股定理得AB2+OA2=OB2,即AB2+32=(AB+1)2,解方程得到AB=4的值,再根据三角函数定义求出sinB.
解答 (1)证明:连接OA、OD,如图,
∵点D为CE的下半圆弧的中点,
∴OD⊥BC,
∴∠EOD=90°,
∵AB=BF,OA=OD,
∴∠BAF=∠BFA,∠OAD=∠D,
而∠BFA=∠OFD,
∴∠OAD+∠BAF=∠D+∠BFA=90°,即∠OAB=90°,
∴OA⊥AB,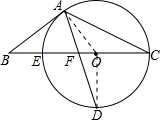 ∴AB是⊙O切线;
∴AB是⊙O切线;
(2)解:OF=CF-OC=4-r,OD=r,DF=$\sqrt{10}$,
在Rt△DOF中,OD2+OF2=DF2,即r2+(4-r)2=($\sqrt{10}$)2,
解得r1=3,r2=1(舍去);
∴半径r=3,
∴OA=3,OF=CF-OC=4-3=1,BO=BF+FO=AB+1.
在Rt△AOB中,AB2+OA2=OB2,
∴AB2+32=(AB+1)2,
∴AB=4,OB=5,
∴sinB=$\frac{OA}{OB}$=$\frac{3}{5}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理以及锐角三角函数的定义.

 小学教材完全解读系列答案
小学教材完全解读系列答案A市七年级部分学生参加社会实践活动天数的频数分布表
| 天数 | 频数 | 频率 |
| 3 | 20 | 0.10 |
| 4 | 30 | 0.15 |
| 5 | 60 | 0.30 |
| 6 | a | 0.25 |
| 7 | 40 | 0.20 |
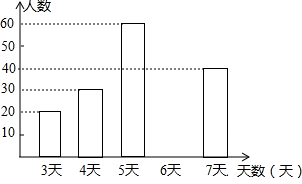
根据以上信息,解答下列问题;
(1)求出频数分布表中a的值,并补全条形统计图.
(2)A市有七年级学生20000人,请你估计该市七年级学生参加社会实践活动不少于5天的人数.
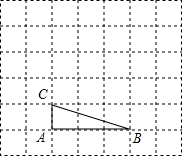 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上. 将下列事件发生的概率填在图中:(只填各事件的序号)
将下列事件发生的概率填在图中:(只填各事件的序号)
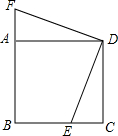 已知,如图,正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF.连接DE、DF.求证:DE=DF.
已知,如图,正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF.连接DE、DF.求证:DE=DF. 如图,点A(m,4),B(-4,n)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
如图,点A(m,4),B(-4,n)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D. 如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为24.
如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为24. 如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.
如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.