题目内容
1. 将一张矩形纸片折叠成如图所示的图形,若AB=6cm,则AC=6cm.
将一张矩形纸片折叠成如图所示的图形,若AB=6cm,则AC=6cm.
分析 延长原矩形的边,然后根据两直线平行,内错角相等可得∠1=∠ACB,根据翻折变换的性质可得∠1=∠ABC,从而得到∠ABC=∠ACB,再根据等角对等边可得AC=AB,从而得解.
解答  解:如图,延长原矩形的边,
解:如图,延长原矩形的边,
∵矩形的对边平行,
∴∠1=∠ACB,
由翻折变换的性质得,∠1=∠ABC,
∴∠ABC=∠ACB,
∴AC=AB,
∵AB=6cm,
∴AC=6cm.
故答案为:6.
点评 本题考查了翻折变换的性质,平行线的性质,等腰三角形的判定,熟记各性质是解题的关键,难点在于作出辅助线.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
16. 如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
 如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )| A. | 34° | B. | 54° | C. | 66° | D. | 56° |
20.以下说法合理的是( )
| A. | 小明在10次抛图钉的试验中发现3次钉朝上,由此他说钉尖朝上的概率是30% | |
| B. | 抛掷一枚普通的正六面体骰子,出现6的概率是$\frac{1}{6}$的意思是每6次就有1次掷得6 | |
| C. | 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖 | |
| D. | 在一次课堂进行的抛掷硬币试验中,某同学估计硬币落地后,正面朝上的概率为$\frac{1}{2}$ |
 将下列事件发生的概率填在图中:(只填各事件的序号)
将下列事件发生的概率填在图中:(只填各事件的序号) 如图,点A(m,4),B(-4,n)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
如图,点A(m,4),B(-4,n)在反比例函数y=$\frac{k}{x}$(k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D. 如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为24.
如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为24.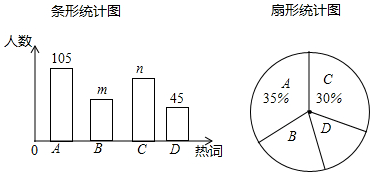
 如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.
如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里. 如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.
如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.