题目内容
1.已知a>b>0,a2+b2=3ab,则$\frac{a+b}{a-b}$的值为$\sqrt{5}$.分析 先依据完全平方公式得到(a+b)2=5ab,(a-b)2=ab,然后由$\frac{a+b}{a-b}$=$\sqrt{\frac{(a+b)^{2}}{(a-b)^{2}}}$求解即可.
解答 解:∵a2+b2=3ab,
∴(a+b)2=5ab,(a-b)2=ab.
∵a>b>0,
∴$\frac{a+b}{a-b}$>0.
∴$\frac{a+b}{a-b}$=$\sqrt{\frac{(a+b)^{2}}{(a-b)^{2}}}$=$\sqrt{\frac{5ab}{ab}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题主要考查的是求分式的值,依据完全平方公式求得$\sqrt{\frac{(a+b)^{2}}{(a-b)^{2}}}$=$\sqrt{5}$是解题的关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
12.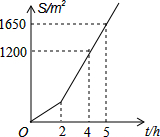 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )| A. | 300m2 | B. | 150m2 | C. | 330m2 | D. | 450m2 |
11.中国的领水面积约为370000km2,其中南海的领水面积约占我国领水面积的$\frac{1}{2}$,用科学记数法表示中国南海的领水面积是( )
| A. | 37×105km2 | B. | 37×104km2 | C. | 0.85×105km2 | D. | 1.85×105km2 |
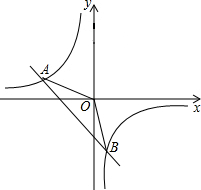 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).