题目内容
10.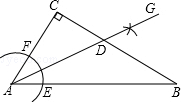 如图,在△ABC中,∠C=90°,∠CAB=56°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D.则∠ADC的度数为( )
如图,在△ABC中,∠C=90°,∠CAB=56°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D.则∠ADC的度数为( )| A. | 34° | B. | 52° | C. | 58° | D. | 62° |
分析 利用基本作图得到AG平分∠CAB,则根据角平分线的定义得到∠CAD的度数,然后根据互余可计算出∠ADC的度数.
解答 解:由作法得AG为∠CAB的角平分线,
∴∠CAD=$\frac{1}{2}$∠CAB=$\frac{1}{2}$×56°=28°,
∴∠ADC=90°-∠CAD=90°-28°=62°.
故选D.
点评 本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
7.设a是最小的自然数,b是最大的负整数,c是绝对值最小的有理数,则a-b+c=( )
| A. | 1 | B. | 2 | C. | 0 | D. | 以上都不对 |
1.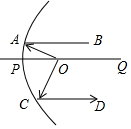 卫星信号接收锅、汽车灯等很多灯具都与抛物线有关,如图,从点O照射到抛物线上的光线OA、OC等反射以后沿着与POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度数是( )
卫星信号接收锅、汽车灯等很多灯具都与抛物线有关,如图,从点O照射到抛物线上的光线OA、OC等反射以后沿着与POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度数是( )
 卫星信号接收锅、汽车灯等很多灯具都与抛物线有关,如图,从点O照射到抛物线上的光线OA、OC等反射以后沿着与POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度数是( )
卫星信号接收锅、汽车灯等很多灯具都与抛物线有关,如图,从点O照射到抛物线上的光线OA、OC等反射以后沿着与POQ平行的方向射出,已知∠OAB=25°,OA⊥OC,那么∠OCD的度数是( )| A. | 65° | B. | 75° | C. | 115° | D. | 135° |
18.点P(-1,2)关于y轴对称的点得坐标为( )
| A. | (1,-2) | B. | (-1,-2) | C. | (1,2) | D. | (2,-1) |
19.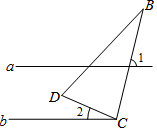 如图所示,已知直线a,b,其中a∥b,点C在直线b上,∠DCB=90°,若∠1=75°,则∠2=( )
如图所示,已知直线a,b,其中a∥b,点C在直线b上,∠DCB=90°,若∠1=75°,则∠2=( )
 如图所示,已知直线a,b,其中a∥b,点C在直线b上,∠DCB=90°,若∠1=75°,则∠2=( )
如图所示,已知直线a,b,其中a∥b,点C在直线b上,∠DCB=90°,若∠1=75°,则∠2=( )| A. | 25° | B. | 15° | C. | 20° | D. | 30° |
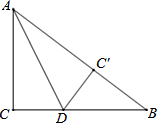 如图,有一块直角三角形ABC纸片,∠ACB=90°,AC=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,点C与点C'重合,求CD的长.
如图,有一块直角三角形ABC纸片,∠ACB=90°,AC=6,BC=8,现将直角边AC沿直线AD折叠,使它落在斜边AB上,点C与点C'重合,求CD的长.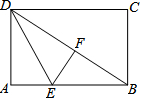 如图,折叠长方形纸片ABCD,先折出对角线BD,再将AD折叠到BD上,得到折痕DE,点A的对应点是点F,若AB=8,BC=6,则AE的长为3.
如图,折叠长方形纸片ABCD,先折出对角线BD,再将AD折叠到BD上,得到折痕DE,点A的对应点是点F,若AB=8,BC=6,则AE的长为3.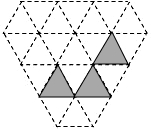 如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的完整图形是一个轴对称图形.
如图所示的“钻石”型网格(由边长都为1个单位长度的等边三角形组成),其中已经涂黑了3个小三角形(阴影部分表示),请你再只涂黑一个小三角形,使它与阴影部分合起来所构成的完整图形是一个轴对称图形.