题目内容
19．
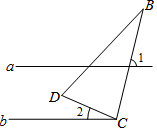如图所示，已知直线a，b，其中a∥b，点C在直线b上，∠DCB=90°，若∠1=75°，则∠2=（ ）| A． | 25° | B． | 15° | C． | 20° | D． | 30° |
分析 先根据对顶角的定义求出∠3的度数，再由平行线的性质即可得出结论．
解答 
解：∵∠1=75°，∠1与∠3是对顶角，
∴∠3=∠1=75°，
∵a∥b，点C在直线b上，∠DCB=90°，
∴∠2+∠DCB+∠3=180°，
∴∠2=180°-∠3-∠DCB=180°-75°-90°=15°．
故选B．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．
练习册系列答案
相关题目
某航空公司托运行李的费用y元与托运行李的质量x（kg）之间的函数关系如图所示，根据图中的信息可知：免费托运行李质量应不超过19kg．
10．
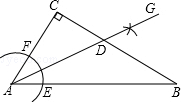如图，在△ABC中，∠C=90°，∠CAB=56°，按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于$\frac{1}{2}$EF长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D．则∠ADC的度数为（ ）
如图，在△ABC中，∠C=90°，∠CAB=56°，按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于$\frac{1}{2}$EF长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D．则∠ADC的度数为（ ）| A． | 34° | B． | 52° | C． | 58° | D． | 62° |
14．2017的绝对值是（ ）
| A． | -2017 | B． | 2017 | C． | $\frac{1}{2017}$ | D． | -$\frac{1}{2017}$ |
4．下列各式从左到右的变形正确的是（ ）
| A． | $\frac{-a+b}{-a-b}=\frac{a+b}{a-b}$ | |
| B． | $\frac{0.4a-0.09b}{0.8c+0.06d}=\frac{4a-9b}{8c+6d}$ | |
| C． | $\frac{{{b^2}-{a^2}}}{a+b}=a-b$ | |
| D． | $\frac{{1-\frac{1}{3}a}}{{a+\frac{1}{5}}}=\frac{15-5a}{15a+3}$ |
8．将二次函数y=x2的图象向左平移1个单位，则平移后的二次函数的解析式为（ ）
| A． | y=x2-1 | B． | y=x2+1 | C． | y=（x-1）2 | D． | y=（x+1）2 |
9．对于命题“如果∠1+∠2=90°，那么∠1≠∠2”，说明它是假命题的反例可以是（ ）
| A． | ∠1=50°，∠2=40° | B． | ∠1=50°，∠2=50° | C． | ∠1=40°，∠2=40° | D． | ∠1=∠2=45° |