题目内容
20.计算或化简(1)计算:|$\sqrt{3}$-2|+20170-($\frac{1}{3}$)-13tan30°;
(2)解方程:x(x+2)=5x+10.
分析 (1)根据实数的混合运算顺序和法则计算可得;
(2)因式分解法求解可得.
解答 解:(1)原式=2-$\sqrt{3}$+1-3×3×$\frac{\sqrt{3}}{3}$
=3-$\sqrt{3}$-3$\sqrt{3}$
=3-4$\sqrt{3}$;
(2)∵x(x+2)-5(x+2)=0,
∴(x+2)(x-5)=0,
则x+2=0或x-5=0,
解得:x1=-2 x2=5.
点评 本题主要考查解一元二次方程的能力和实数的混合运算,熟练掌握实数的混合运算顺序和法则和解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
10.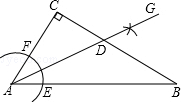 如图,在△ABC中,∠C=90°,∠CAB=56°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D.则∠ADC的度数为( )
如图,在△ABC中,∠C=90°,∠CAB=56°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D.则∠ADC的度数为( )
 如图,在△ABC中,∠C=90°,∠CAB=56°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D.则∠ADC的度数为( )
如图,在△ABC中,∠C=90°,∠CAB=56°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;③作射线AG,交BC边于点D.则∠ADC的度数为( )| A. | 34° | B. | 52° | C. | 58° | D. | 62° |
8.将二次函数y=x2的图象向左平移1个单位,则平移后的二次函数的解析式为( )
| A. | y=x2-1 | B. | y=x2+1 | C. | y=(x-1)2 | D. | y=(x+1)2 |
9.对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,说明它是假命题的反例可以是( )
| A. | ∠1=50°,∠2=40° | B. | ∠1=50°,∠2=50° | C. | ∠1=40°,∠2=40° | D. | ∠1=∠2=45° |
10.下列计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (b-a)2=b2-2ab+a2 | C. | (a+2b)(a-2b)=a2-2b2 | D. | (a-b)2=a2-2ab-b2 |
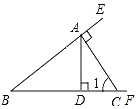 如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:
如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论: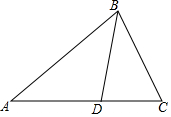 已知:如图,在△ABC中,D是AC上一点,$\frac{CB}{CD}$=$\frac{CA}{CB}$=$\frac{3}{2}$,△BCD的周长是24cm.
已知:如图,在△ABC中,D是AC上一点,$\frac{CB}{CD}$=$\frac{CA}{CB}$=$\frac{3}{2}$,△BCD的周长是24cm.