题目内容
15．
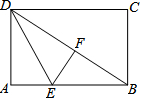如图，折叠长方形纸片ABCD，先折出对角线BD，再将AD折叠到BD上，得到折痕DE，点A的对应点是点F，若AB=8，BC=6，则AE的长为3．
分析 先利用勾股定理求出BD，再求出DF、BF，设AE=EF=x，在Rt△BEF中，由EB2=EF2+BF2，列出方程即可解决问题．
解答 解：∵四边形ABCD是矩形，
∴∠A=90°，
∵AB=8，AD=6，
∴BD=$\sqrt{{6}^{2}+{8}^{2}}$=10，
∵△DEF是由△DEA翻折得到，
∴DF=AD=6，BF=4，
设AE=EF=x，
在Rt△BEF中，∵EB2=EF2+BF2，
∴（8-x）2=x2+42，
解得x=3，
∴AE=3，
故答案为3．
点评 本题考查矩形的性质、勾股定理等知识，解题时，我们常常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．
练习册系列答案
相关题目
12．下列运算正确的是（ ）
| A． | a5+a5=a10 | B． | a7•a6=a42 | C． | a4-a4=a0 | D． | a0÷a-1=a |
10．
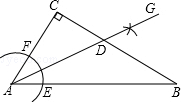如图，在△ABC中，∠C=90°，∠CAB=56°，按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于$\frac{1}{2}$EF长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D．则∠ADC的度数为（ ）
如图，在△ABC中，∠C=90°，∠CAB=56°，按以下步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于$\frac{1}{2}$EF长为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D．则∠ADC的度数为（ ）| A． | 34° | B． | 52° | C． | 58° | D． | 62° |
20．在△ABD与△ACD中，∠BAD=∠CAD，且B点，C点在AD边两侧，则不一定能使△ABD和△ACD全等的条件是（ ）
| A． | BD=CD | B． | ∠B=∠C | C． | AB=AC | D． | ∠BDA=∠CDA |
4．下列各式从左到右的变形正确的是（ ）
| A． | $\frac{-a+b}{-a-b}=\frac{a+b}{a-b}$ | |
| B． | $\frac{0.4a-0.09b}{0.8c+0.06d}=\frac{4a-9b}{8c+6d}$ | |
| C． | $\frac{{{b^2}-{a^2}}}{a+b}=a-b$ | |
| D． | $\frac{{1-\frac{1}{3}a}}{{a+\frac{1}{5}}}=\frac{15-5a}{15a+3}$ |
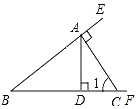如图，已知点A是射线BE上一点，过A作CA⊥BE交射线BF于点C，AD⊥BF交射线BF于点D，给出下列结论：