题目内容
5.下列说法正确的是( )| A. | 两边和一角对应相等的两三角形全等 | |
| B. | 两边对应相等的两个三角形全等 | |
| C. | 一锐角和一边对应相等的两个直角三角形全等 | |
| D. | 所有的等边三角形都全等 |
分析 根据三角形的判定方法SSS、SAS、ASA、AAS、HL进行分析可得答案.
解答 解:A、两边和一角对应相等的两三角形全等,说法错误;
B、两边对应相等的两个三角形全等,说法错误;
C、一锐角和一边对应相等的两个直角三角形全等,说法正确;
D、所有的等边三角形都全等,说法错误;
故选:C.
点评 此题主要考查了全等三角形的判定,熟练掌握三角形的判定定理是解题的关键.

练习册系列答案
相关题目
16.某地区人口状况相对稳定,人寿保险公司根据多年统计综合,有一张关于该地区人口寿命的表格,现摘录部分内容如下.
根据上表解答下列各题:
(1)该地区达到50岁的人中,不能达到51岁的概率约是多少?能达到80岁的概率约为多少?(精确到0.001)
(2)如果有20000个50岁的人参加人寿保险,当年死亡的赔偿金均为10万元,预计保险公司需付这一项赔偿的总额为多少?
| 年龄 | 到达该年龄的人数 | 在该年龄死亡的人数 |
| 40 | 80500 | 892 |
| 50 | 78009 | 951 |
| 60 | 69891 | 1200 |
| 70 | 45502 | 2199 |
| 80 | 16078 | 2001 |
| … | … | … |
(1)该地区达到50岁的人中,不能达到51岁的概率约是多少?能达到80岁的概率约为多少?(精确到0.001)
(2)如果有20000个50岁的人参加人寿保险,当年死亡的赔偿金均为10万元,预计保险公司需付这一项赔偿的总额为多少?
10.二次函数y=ax2+bx+c的部分对应值如下表:
二次函数y=ax2+bx+c图象的对称轴为x=2,x=-1对应的函数值y=-22.
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | -54 | -36 | -12 | -6 | -6 | -22 | … |
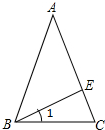 已知:如图,在△ABC中,AB=AC,∠1=$\frac{1}{2}$∠BAC,求证:BE⊥AC.
已知:如图,在△ABC中,AB=AC,∠1=$\frac{1}{2}$∠BAC,求证:BE⊥AC. 如图所示,∠ACB=90°,CD⊥AB,∠1与∠A,∠2与∠B有什么关系?用一个命题表达你所得到的结论为等角的余角相等.
如图所示,∠ACB=90°,CD⊥AB,∠1与∠A,∠2与∠B有什么关系?用一个命题表达你所得到的结论为等角的余角相等.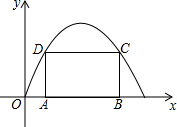 如图,已知抛物线y=ax2+bx+c经过原点O,它的顶点坐标为(5,$\frac{25}{4}$),在抛物线内作矩形ABCD,使顶点C,D落在抛物线上,顶点A,B落在x轴上.
如图,已知抛物线y=ax2+bx+c经过原点O,它的顶点坐标为(5,$\frac{25}{4}$),在抛物线内作矩形ABCD,使顶点C,D落在抛物线上,顶点A,B落在x轴上.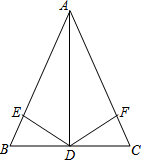 如图,△ABC中,AD是它的角平分线,且BD=CD,DE、DF分别垂直于AB、AC于E、F.求证:(1)△AED≌△ADF;(2)BE=CF.
如图,△ABC中,AD是它的角平分线,且BD=CD,DE、DF分别垂直于AB、AC于E、F.求证:(1)△AED≌△ADF;(2)BE=CF. 已知:如图,在⊙O中,弧AB=弧BC=弧CD,OB,OC分别交AC、BD于E、F,则下列结论:①OE=BE;②OC⊥BD;③AE=DF;④OE=OF中正确的有②③④(填序号)
已知:如图,在⊙O中,弧AB=弧BC=弧CD,OB,OC分别交AC、BD于E、F,则下列结论:①OE=BE;②OC⊥BD;③AE=DF;④OE=OF中正确的有②③④(填序号)