题目内容
20.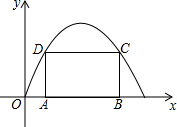 如图,已知抛物线y=ax2+bx+c经过原点O,它的顶点坐标为(5,$\frac{25}{4}$),在抛物线内作矩形ABCD,使顶点C,D落在抛物线上,顶点A,B落在x轴上.
如图,已知抛物线y=ax2+bx+c经过原点O,它的顶点坐标为(5,$\frac{25}{4}$),在抛物线内作矩形ABCD,使顶点C,D落在抛物线上,顶点A,B落在x轴上.(1)求抛物线对应的函数表达式;
(2)若AB=6,求AD的长;
(3)设矩形ABCD的周长为l,求l的最大值.
分析 (1)利用图象上顶点坐标以及原点,由顶点式求出二次函数解析式即可;
(2)根据已知得出D点横坐标x=2,求出D点纵坐标即可得出AD的长;
(3)首先表示出矩形周长,再利用二次函数最值公式求出.
解答 解:(1)根据坐标系可知此函数顶点坐标为(5,$\frac{25}{4}$),且图象过(0,0)点,
代入顶点式得:
y=a(x-5)2+$\frac{25}{4}$,
将(0,0)代入解析式得:
∴0=a(0-5)2+$\frac{25}{4}$,
解得:a=-0.25,
∴y=-0.25(x-5)2+$\frac{25}{4}$;
(2)∵此函数顶点坐标为(5,$\frac{25}{4}$),且图象过(0,0)点,
∴图象与x轴另一交点为:(10,0),
当AB=6时,
∴AO=(10-6)÷2=2,
∴x=2代入解析式得:
y=-0.25(2-5)2+6.25;
y=4,
∴AD=4;
(3)假设AO=x,可得AB=10-2x,
∴AD=-0.25(x-5)2+6.25;
∴矩形ABCD的周长为l为:l=2[-0.25(x-5)2+6.25]+2(10-2x)=-0.5x2+x+20,
∴l的最大值为:$\frac{4ac-{b}^{2}}{4a}$=$\frac{-40-1}{-2}$=20.5.
点评 此题主要考查了顶点式求二次函数解析式以及二次函数最值求法,根据函数图象获取正确点的坐标以及利用图象上点的性质是解决问题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
5.下列说法正确的是( )
| A. | 两边和一角对应相等的两三角形全等 | |
| B. | 两边对应相等的两个三角形全等 | |
| C. | 一锐角和一边对应相等的两个直角三角形全等 | |
| D. | 所有的等边三角形都全等 |
 据新华社报道,某省4艘渔船在回港途中,遭遇9级强风,岛上边防战士接到命令后立即准备搜救.你能告诉边防战士这些渔船的位置吗?
据新华社报道,某省4艘渔船在回港途中,遭遇9级强风,岛上边防战士接到命令后立即准备搜救.你能告诉边防战士这些渔船的位置吗? 如图,直径AB=4,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥AB,垂足为E、F.求EF的长.
如图,直径AB=4,半径OC⊥AB,D为弧AC上一点,DE⊥OC,DF⊥AB,垂足为E、F.求EF的长.