题目内容
3.在方程组$\left\{\begin{array}{l}{x+y=m}\\{2x-y=6}\end{array}\right.$中.(1)若已知x>0,y<0,求m的取值范围;
(2)若xy<0,且x,y都是整数,求m的取值.
分析 (1)要求m的取值范围也要先求出x,y的值,然后由给出的x>0,y<0,列出不等式方程组,再解不等式方程即可;
(2)根据xy<0,列出不等式,求出m的取值范围,根据x,y都是整数,确定m的取值,即可解答.
解答 解:(1)方程组$\left\{\begin{array}{l}{x+y=m}\\{2x-y=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{m+6}{3}}\\{y=\frac{2m-6}{3}}\end{array}\right.$,
∵x>0,y<0,
∴$\left\{\begin{array}{l}{\frac{m+6}{3}>0}\\{\frac{2m-6}{3}<0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m>-6}\\{m<3}\end{array}\right.$,
∴-6<m<3.
(2)∵xy<0,
∴$\frac{m+6}{3}•\frac{2m-6}{3}<0$,
m2+3m-18<0
∴-6<m<3,
∴m为整数-5,-4,-3,-2,-1,0,1,2,
∵x,y都是整数,
∴m+6与2m-6都应为3的倍数,
∴m=-3,0.
点评 本题考查了二元一次方程组的解,解决本题的关键是根据已知条件列出不等式组.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.在函数y=$\frac{{\sqrt{x+1}}}{x-2}$中,自变量x的取值范围是( )
| A. | x≤-1 | B. | x≥-1 | C. | x≤-1且x≠2 | D. | x≥-1且x≠2 |
10.一个质地均匀的正方体骰子的六个面上分别刻有“我”、“爱”、“爸”、“爸”、“妈”、“妈”六个字,如果将这个骰子掷一次,那么向上一面出现“妈”字的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
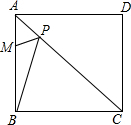 已知正方形ABCD的一条对角线长为6,M是边AB的一个点,且AM:MB=1:2;P是对角线AC上的一个动点,则PM+PB的最小值=2$\sqrt{5}$.
已知正方形ABCD的一条对角线长为6,M是边AB的一个点,且AM:MB=1:2;P是对角线AC上的一个动点,则PM+PB的最小值=2$\sqrt{5}$.