题目内容
1.已知关于x,y的方程组$\left\{\begin{array}{l}{3x-y=k}\\{2x+3y=2k-1}\end{array}\right.$的解满足不等式$\left\{\begin{array}{l}{x-4y≥0}\\{5x+2y≥-2}\end{array}\right.$,求满足条件的k的整数值.分析 将k看做已知数表示出x与y,代入已知不等式组即可求出k的范围,即可确定整数值.
解答 解:方程组$\left\{\begin{array}{l}{3x-y=k}\\{2x+3y=2k-1}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=\frac{5k-1}{11}}\\{y=\frac{4k-3}{11}}\end{array}\right.$,
把$\left\{\begin{array}{l}{x=\frac{5k-1}{11}}\\{y=\frac{4k-3}{11}}\end{array}\right.$代入不等式$\left\{\begin{array}{l}{x-4y≥0}\\{5x+2y≥-2}\end{array}\right.$得:
$\left\{\begin{array}{l}{-11k+12≤0}\\{3k+11≥0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k≤\frac{12}{11}}\\{k≥-\frac{11}{3}}\end{array}\right.$,
∴$-\frac{11}{3}≤k≤\frac{12}{11}$.
∴k=-3,-2,-1,0,1.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值,解决本题的关键是求出方程组的解,列出不等式组.

练习册系列答案
相关题目
16.x,y的方程组$\left\{\begin{array}{l}{x+y=2a+7}\\{x-2y=4a-3}\end{array}\right.$的解为正数,且x的值小于y的值,求a的取值范围.
6.2015年浙江省公务员考试计划录用9525名.数9525用科学记数法表示为( )
| A. | 9.525×103 | B. | 0.9525×104 | C. | 95.25×103 | D. | 95.25×102 |
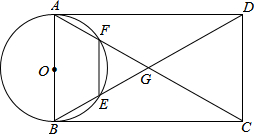 平行四边形ABCD两条对角线交于点G,∠DBC=∠ACB,以AB为直径作⊙O,分别交BD、AC于点E、点F,点E、点F分别是$\widehat{AB}$的三等分点,当BC=6时,求EF的长.
平行四边形ABCD两条对角线交于点G,∠DBC=∠ACB,以AB为直径作⊙O,分别交BD、AC于点E、点F,点E、点F分别是$\widehat{AB}$的三等分点,当BC=6时,求EF的长. 如图,△ABC中,∠BAC=40°,∠B=60°,且AP∥BC,则∠1的度数为80°.
如图,△ABC中,∠BAC=40°,∠B=60°,且AP∥BC,则∠1的度数为80°.