题目内容
1.已知x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}$-$\sqrt{2}$,求(1)x2-xy+y2;
(2)x3y+xy3的值.
分析 (1)首先把已知的式子进行变形,变形后代入数值计算即可求解;
(2)首先把所求的式子进行分解因式,然后代入数值计算即可求解.
解答 解:(1)因为x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}$-$\sqrt{2}$,
可得:x2-xy+y2=(x+y)2+xy=$(\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2})^{2}+(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})=13$;
(2)因为x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}$-$\sqrt{2}$,
可得:x3y+xy3=xy[(x+y)2-2xy]
=$(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})[(\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2})^{2}-2(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})]$=10
点评 本题考查了二次根式的化简求值,正确对所求的式子进行变形是关键.

练习册系列答案
相关题目
9.侧面展开图是一个长方形的几何体的是( )
| A. | 圆锥 | B. | 圆柱 | C. | 四棱柱 | D. | 球体 |
6.来自城市自来水收费实行阶梯水价,收费标准如下表所示:
某户5月份用水x(x>18)吨,则水费为多少元?若用水28吨,则水费多少元?
| 月用水量 | 不超过12吨的部分 | 超过12吨不超过18吨的部分 | 超过18吨的部分 |
| 收费标准(元/吨) | 2.00 | 2.50 | 3.00 |
11.若(3x+a)(3x+b)的结果中不含有x项,则a、b的关系是( )
| A. | ab=1 | B. | ab=0 | C. | a-b=0 | D. | a+b=0 |
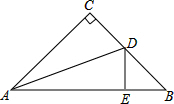 如图,在Rt△ABC中,已知∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若△BDE的周长为8,则AB的长为8.
如图,在Rt△ABC中,已知∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若△BDE的周长为8,则AB的长为8.